Question

【題目】在平面直角坐標系中，拋物線與軸交于點，，與軸交于點，直線經(jīng)過，兩點．

求拋物線的解析式；

在上方的拋物線上有一動點．

①如圖，當點運動到某位置時，以，為鄰邊的平行四邊形第四個頂點恰好也在拋物線上，求出此時點的坐標；

②如圖，過點，的直線交于點，若，求的值．

Answer 1

【答案】（1）；（2）①點的坐標是；②．

【解析】

（1）由直線的解析式y=x+4易求點A和點C的坐標，把A和C的坐標分別代入y=- x2+bx+c求出b和c的值即可得到拋物線的解析式；

（2）①若以AP，AO為鄰邊的平行四邊形的第四個頂點Q恰好也在拋物線上，則PQ∥AO，再根據(jù)拋物線的對稱軸可求出點P的橫坐標，由（1）中的拋物線解析式，進而可求出其縱坐標，問題得解；

②過P點作PF∥OC交AC于點F，因為PF∥OC，所以△PEF∽△OEC，由相似三角形的性質：對應邊的比值相等可求出PF的長，進而可設點點F（x，x+4），利用(x2x+4)(x+4)＝，可求出x的值，解方程求出x的值可得點P的坐標，代入直線y=kx即可求出k的值．

解：∵直線經(jīng)過，兩點，

∴點坐標是，點坐標是，

又∵拋物線過，兩點，

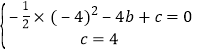∴，解得：，

∴拋物線的解析式為．

①如圖

∵，

∴拋物線的對稱軸是直線．

∵以，為鄰邊的平行四邊形的第四個頂點恰好也在拋物線上，

∴，．

∵，都在拋物線上，

∴，關于直線對稱，

∴點的橫坐標是，

∴當時，，

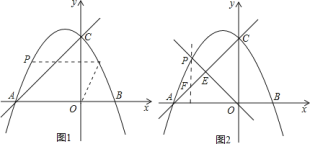
∴點的坐標是；

②過點作交于點，

∵，

∴，

∴．

又∵，

∴，

設點，

∴，

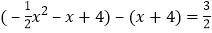化簡得：，解得：，．

當時，；當時，，

即點坐標是或．

又∵點在直線上，

∴．