
【題目】在平面直角坐標系![]() 中,將
中,將![]() (
(![]() )沿直線
)沿直線![]() 運動到點
運動到點![]() ,若點
,若點![]() 的坐標為
的坐標為![]() ,則稱點
,則稱點![]() 為點
為點![]() 的“鉛直變換點”。
的“鉛直變換點”。
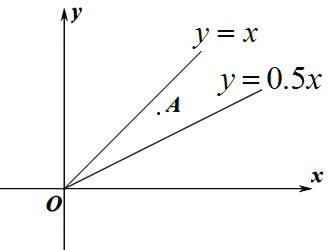
(1) 點![]() 的鉛直變換點坐標___________;一個點的鉛直變換點是
的鉛直變換點坐標___________;一個點的鉛直變換點是![]() ,則這個點的坐標_________
,則這個點的坐標_________
(2) 已知點![]() 的坐標為(
的坐標為(![]() ). 點
). 點![]() 在一次函數
在一次函數![]() 的圖像上,點
的圖像上,點![]() 的鉛直變換點為點
的鉛直變換點為點![]() ,若這三個點中,其中的兩個點關于另一點成中心對稱,求
,若這三個點中,其中的兩個點關于另一點成中心對稱,求![]() 的值.
的值.
(3) 已知點![]() 在一次函數
在一次函數![]() 和一次函數
和一次函數![]() 的圖像所組成的角的內部,它的鉛直變換點為點B,且
的圖像所組成的角的內部,它的鉛直變換點為點B,且![]() 滿足
滿足![]() ,判斷線段
,判斷線段![]() 的長度能否等于
的長度能否等于![]() ,若能,求點
,若能,求點![]() 的坐標,若不能,請說明理由。
的坐標,若不能,請說明理由。
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ; (3) 不能
; (3) 不能
【解析】
(1)根據“鉛直變換點”的定義即可求解;
(2)根據“鉛直變換點”的定義寫出B點坐標,再根據中心對稱的特點分情況討論;
(3)根據A點處于夾角內部得到![]() <b<a,得到a-b>0,B點坐標為(a,a-b),根據
<b<a,得到a-b>0,B點坐標為(a,a-b),根據![]() =a-b得到
=a-b得到![]() <
<![]() ,求出a的取值,再得到b>a-b,從而得到AB的長度,根據
,求出a的取值,再得到b>a-b,從而得到AB的長度,根據![]() 的長度為
的長度為![]() 得到a,b之間的關系,再代入
得到a,b之間的關系,再代入![]() ,根據根的判別式即可求解.
,根據根的判別式即可求解.
(1)點![]() 的鉛直變換點坐標為(4,4-3),即為
的鉛直變換點坐標為(4,4-3),即為![]() ;
;
一個點的鉛直變換點是![]() ,即
,即![]() ,則這個點的坐標為
,則這個點的坐標為![]() ;
;
故填:![]() ,
,![]() ;
;
(2)∵點![]() 的坐標為(
的坐標為(![]() ). 點
). 點![]() 在一次函數
在一次函數![]() 的圖像上,
的圖像上,
∴點![]() (a,b+1),∴A的鉛直變換點為點
(a,b+1),∴A的鉛直變換點為點![]() (a,1),
(a,1),
①若A,B關于C成中心對稱,則![]()
解得a=![]()
②若C,B關于A成中心對稱,則![]()
解得a=3
③若A,C關于B成中心對稱,則![]()
解得a=![]()
故![]() 時這三個點中,其中的兩個點關于另一點成中心對稱;
時這三個點中,其中的兩個點關于另一點成中心對稱;
(3)不能,理由如下:
根據A點處于夾角內部得到![]() <b<a,
<b<a,
∴a-b>0,
∵A(a,b)
∴B點坐標為(a,a-b),
∵![]() ,
,
∴a-b=![]() ,
,
∵![]() <b
<b
∴a-![]() <b
<b
∴a-b<![]()
即![]() <
<![]()
故a(2a-1)<0,
根據二次函數圖像可得a的取值為0<a<![]() ;
;
又![]() <b<a,
<b<a,
∴b>a-b,
故AB=b-(a-b)=2b-a= ![]()
得到b=![]()
代入![]() ,得
,得![]()
△=16-4×8=-16<0,
故a無解,即![]() 的長度不能等于
的長度不能等于![]() .
.


 新活力總動員暑系列答案
新活力總動員暑系列答案 龍人圖書快樂假期暑假作業鄭州大學出版社系列答案
龍人圖書快樂假期暑假作業鄭州大學出版社系列答案科目:初中數學 來源: 題型:
【題目】某賓館有50個房間供游客住宿,當每個房間的房價為每天180元時,房間會全部住滿.當每個房間 每天的房價每增加10元時,就會有一個房間空閑.賓館需對游客居住的每個房間每天支出20元的各種費用.根據規定,每個房間每天的房價不得高于340元.設每個房間的房價增加x元(x為10的正整數倍).
(1)設一天訂住的房間數為y,直接寫出y與x的函數關系式及自變量x的取值范圍;
(2)設賓館一天的利潤為w元,求w與x的函數關系式;
(3)一天訂住多少個房間時,賓館的利潤最大?最大利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數![]() 的大致圖象如圖所示,關于該二次函數,下列說法錯誤的是( )
的大致圖象如圖所示,關于該二次函數,下列說法錯誤的是( )
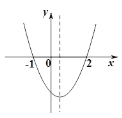
A.函數有最小值B.圖象對稱軸是直線x=![]()
C.當x<![]() ,y隨x的增大而減小D.當-1<x<2時,y>0
,y隨x的增大而減小D.當-1<x<2時,y>0
查看答案和解析>>
科目:初中數學 來源: 題型:
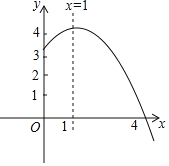
【題目】拋物線![]() 的部分圖象如圖所示,與
的部分圖象如圖所示,與![]() 軸的一個交點坐標為
軸的一個交點坐標為![]() ,拋物線的對稱軸是直線
,拋物線的對稱軸是直線![]() 。給出下列結論:①
。給出下列結論:①![]() ;②
;②![]() ;③方程
;③方程![]() 有兩個不相等的實數根;④拋物線與x軸的另一個交點坐標為
有兩個不相等的實數根;④拋物線與x軸的另一個交點坐標為![]() ,其中正確的結論有。其中正確的有_____________。(只需填寫序號即可)
,其中正確的結論有。其中正確的有_____________。(只需填寫序號即可)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】共享單車逐漸成為市民喜愛的“綠色出行” 方式之一,今年國慶假期某一天,濟川中學初三數學社團的同學們隨機調查了一個社區,將這天部分出行市民使用共享單車的數據整理成如下統計表.
使用次數 | 0 | 1 | 2 | 3 | 4 | 5 |
人數 | 11 | 15 | 23 | 28 | 18 | 5 |
(1) 這天部分出行市民使用共享單車次數的中位數是__________,眾數是__________
(2) 這天部分出行市民平均每人使用共享單車多少次?
(3) 若該社區這天有1500人出行,請你估計這天使用共享單車次數在3次以上(含3 次)的市民有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
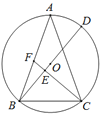
【題目】如圖,△ABC內接于⊙O,AB=AC,CF垂直直徑BD于點E,交邊AB于點F.
(1)求證:∠BFC=∠ABC.
(2)若⊙O的半徑為5,CF=6,求AF長.
查看答案和解析>>
科目:初中數學 來源: 題型:
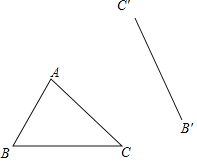
【題目】如圖,求作△ABC繞某點旋轉一定角度后的△A′B′C′時,某同學只作了一部分圖形.
(1)請把△A′B′C′作完整,并保留作圖痕跡;
(2)寫出基本作圖步驟.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】二次函數y=ax2+bx+c的圖象如圖所示,其對稱軸為x=1,有下列結論:①abc<0;②b<a+c;③4a+2b+c<0;④a+b≥m(am+b),其中正確的結論有( )

A.①②B.②③C.①④D.②④
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com