
 如圖,已知雙曲線
如圖,已知雙曲線 (k為常數)與直線l相交于A、B兩點,第一象限內的點M(點M在A的左側)是雙曲線
(k為常數)與直線l相交于A、B兩點,第一象限內的點M(點M在A的左側)是雙曲線 上的一動點,設直線AM、BM分別與y軸交于P、Q兩點.
上的一動點,設直線AM、BM分別與y軸交于P、Q兩點.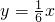 ,A點的坐標為(a,1),
,A點的坐標為(a,1),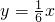 上,
上,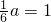 ,
, 上,
上,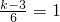 ,
,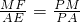 ,即
,即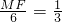 ,
,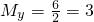 ,
,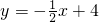 .
.
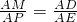 ,即
,即 ,得
,得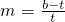 ①
①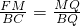 ,即
,即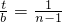 ,得
,得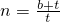

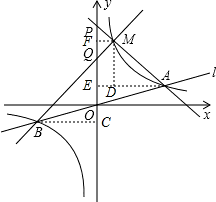
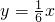 上,得
上,得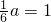 ,解得a=6,然后根據A(6,1)在雙曲線
,解得a=6,然后根據A(6,1)在雙曲線 上解得k=9;
上解得k=9;

科目:初中數學 來源: 題型:
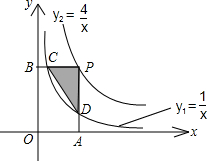 如圖,已知雙曲線y1=
如圖,已知雙曲線y1=| 1 |
| x |
| 4 |
| x |
| 4 |
| x |
| 1 |
| x |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2012•濟南)如圖,已知雙曲線y=
(2012•濟南)如圖,已知雙曲線y=| k | x |
查看答案和解析>>
科目:初中數學 來源: 題型:
 (2013•徐州模擬)如圖,已知雙曲線y=
(2013•徐州模擬)如圖,已知雙曲線y=| k |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:
 如圖,已知雙曲線y=
如圖,已知雙曲線y=| k |
| x |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com