
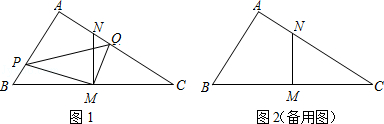
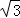 厘米的速度運動.同時,動點Q從點N出發沿射線NC運動,且始終保持MQ丄MP.設運動時間為t秒(t>0).
厘米的速度運動.同時,動點Q從點N出發沿射線NC運動,且始終保持MQ丄MP.設運動時間為t秒(t>0).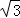 厘米.
厘米.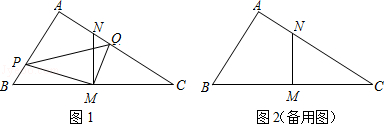
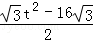
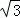 厘米,
厘米,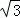 cm,AC=12cm.
cm,AC=12cm.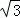 ,
,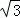 cm.
cm.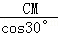 =8cm,
=8cm,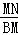 =
=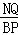 ,
,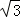 ﹣
﹣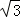 t,
t,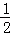 AP•AQ=
AP•AQ=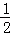 (4
(4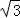 ﹣
﹣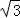 t)(4+t)=
t)(4+t)=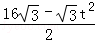 ,
,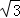 t﹣4
t﹣4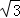 =(t﹣4)
=(t﹣4)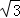 .
. AP•AQ=
AP•AQ= (
(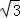 t﹣4
t﹣4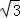 )(4+t)=
)(4+t)=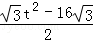 .
.

 期末沖刺100分創新金卷完全試卷系列答案
期末沖刺100分創新金卷完全試卷系列答案科目:初中數學 來源:不詳 題型:解答題
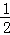 ,以點C為圓心,CB為半徑的弧交CA于點D;以點A為圓心,AD為半徑的弧交AB于點E.
,以點C為圓心,CB為半徑的弧交CA于點D;以點A為圓心,AD為半徑的弧交AB于點E.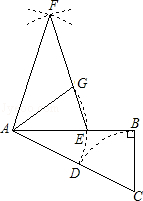
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
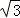 ,AC,BD相交于點O.
,AC,BD相交于點O.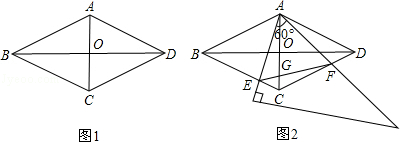
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
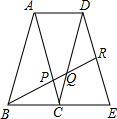
 ,AB=AC=2
,AB=AC=2 .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com