

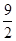 (2)見解析
(2)見解析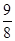 .
.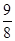 cm
cm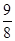 +1.5+
+1.5+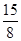 =
=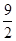


科目:初中數學 來源:不詳 題型:填空題
查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題

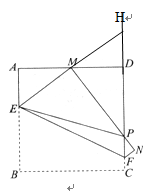
 ,G是EF的中點(如圖2),直接寫出∠BDG的度數;
,G是EF的中點(如圖2),直接寫出∠BDG的度數; ,FG∥CE,
,FG∥CE, ,分別連結DB、DG(如圖3),求∠BDG的度數。
,分別連結DB、DG(如圖3),求∠BDG的度數。查看答案和解析>>
科目:初中數學 來源:不詳 題型:解答題
 和菱形
和菱形 中,點
中,點 在同一條直線上,
在同一條直線上, 是線段
是線段 的中點,連結
的中點,連結 .探究
.探究 與
與 的位置關系及
的位置關系及 的值.小聰同學的思路是:延長
的值.小聰同學的思路是:延長 交
交 于點
于點 ,構造全等三角形,經過推理使問題得到解決.
,構造全等三角形,經過推理使問題得到解決.
 ,寫出線段
,寫出線段 與
與 的位置關系及
的位置關系及 的值,并說明理由;
的值,并說明理由; 繞點
繞點 順時針旋轉,使菱形
順時針旋轉,使菱形 的對角線
的對角線 恰好與菱形
恰好與菱形 的邊
的邊 在同一條直線上,原問題中的其他條件不變(如圖13).你在(1)中得到的兩個結論是否發生變化?寫出你的猜想并加以證明.
在同一條直線上,原問題中的其他條件不變(如圖13).你在(1)中得到的兩個結論是否發生變化?寫出你的猜想并加以證明. ,將菱形
,將菱形 繞點
繞點 順時針旋轉任意角度,原問題中的其他條件不變,請你直接寫出
順時針旋轉任意角度,原問題中的其他條件不變,請你直接寫出 的值(用含
的值(用含 的式子表示).
的式子表示). 與
與 的位置關系是 ;
的位置關系是 ; .
.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com