
【題目】在一個邊長為a(單位:cm)的正方形ABCD中,點E、M分別是線段AC、CD上的動點,連結DE并延長交正方形的邊于點F,過點M作MN⊥DF于H,交AD于N

(1) 如圖①,當點M與點C重合,求證:DF=MN;
(2) 如圖②,假設點M從點C出發,以1 cm/s的速度沿CD向點D運動,點E同時從點A出發,以![]() cm/s速度沿AC向點C運動,運動時間為t(t>0)
cm/s速度沿AC向點C運動,運動時間為t(t>0)
① 判斷命題“當點F是邊AB中點時,則點M是邊CD的三等分點”的真假,并說明理由.
② 連結FM、FN,△MNF能否為等腰三角形?若能,請寫出a、t之間的關系;若不能,請說明理由
【答案】(1)證明見解析;(2)①該命題是真命題.理由見解析;②能.理由見解析;
【解析】
試題分析:(1)證明△ADF≌△DNC,即可得到DF=MN;
(2)①首先證明△AFE∽△CDE,利用比例式求出時間t=![]() a,進而得到CM=
a,進而得到CM=![]() a=
a=![]() CD,所以該命題為真命題;
CD,所以該命題為真命題;
②若△MNF為等腰三角形,則可能有三種情形,需要分類討論.
試題解析:(1)∵∠DNC+∠ADF=90°,∠DNC+∠DCN=90°,
∴∠ADF=∠DCN.
在△ADF與△DNC中,
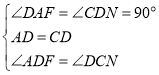 ,
,
∴△ADF≌△DNC(ASA),
∴DF=MN.
(2)①該命題是真命題.
理由如下:當點F是邊AB中點時,則AF=![]() AB=
AB=![]() CD.
CD.
∵AB∥CD,∴△AFE∽△CDE,
∴![]() ,
,
∴AE=![]() EC,則AE=
EC,則AE=![]() AC=
AC=![]() a,
a,
∴t=![]() =
=![]() a.
a.
則CM=1![]() t=
t=![]() a=
a=![]() CD,
CD,
∴點M為邊CD的三等分點.
②能.理由如下:
易證△AFE∽△CDE,∴![]() ,即
,即![]() ,得AF=
,得AF=![]() .
.
易證△MND∽△DFA,∴![]() ,即
,即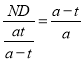 ,得ND=t.
,得ND=t.
∴ND=CM=t,AN=DM=a-t.
若△MNF為等腰三角形,則可能有三種情形:
(Ⅰ)若FN=MN,則由AN=DM知△FAN≌△NDM,
∴AF=ND,即![]() =t,得t=0,不合題意.
=t,得t=0,不合題意.
∴此種情形不存在;
(Ⅱ)若FN=FM,由MN⊥DF知,HN=HM,∴DN=DM=MC,
∴t=![]() a,此時點F與點B重合;
a,此時點F與點B重合;
(Ⅲ)若FM=MN,顯然此時點F在BC邊上,如下圖所示:
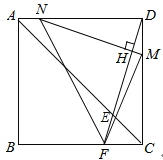
∵AN=DM,AD=CD,
∴ND=CM,
∵![]() ,
,
∴△MFC≌△NMD,∴FC=DM=a-t;
又由△NDM∽△DCF,∴![]() ,即
,即![]() ,∴FC=
,∴FC=![]() .
.
∴![]() =a-t,
=a-t,
∴t=a,此時點F與點C重合.
綜上所述,當t=a或t=![]() a時,△MNF能夠成為等腰三角形.
a時,△MNF能夠成為等腰三角形.


 靈星計算小達人系列答案
靈星計算小達人系列答案 孟建平錯題本系列答案
孟建平錯題本系列答案科目:初中數學 來源: 題型:
【題目】某商店上月的營業額是a萬元,本月比上月增長15%,則本月營業額是( )
A. 15%(a+1)萬元 B. 15% a萬元 C. (1+15%)a萬元 D. (1+15%)2a萬元
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一條船從海島A出發,以25海里/時的速度向正東方向航行,2小時后到達海島B處,從A、B望燈塔C,測得∠DBC=68°,∠DAC=34°,求海島B與燈塔C的距離.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知正方形ABC1D1的邊長為1,延長C1D1到A1,以A1C1為邊向右作正方形A1C1C2D2,延長C2D2到A2,以A2C2為邊向右作正方形A2C2C3D3(如圖所示),以此類推…,若A1C1=2,且點A,D2, D3,…,D10都在同一直線上,則正方形A9C9C10D10的邊長是______
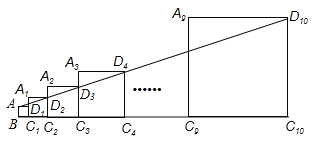
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某次知識競賽共有20道題,每答對一題得10分,答錯或不答都扣5分,娜娜得分要不低于80分,設她答對了x道題,則根據題意可列不等式為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某種微粒子,測得它的質量為0.00006746克,這個質量用科學計數法表示(保留三個有效數字)應為
A. 6.75×10-5克 B. 6.74×10-5克 C. 6.74×10-6克 D. 6.75×10-6克
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com