【題目】附加題：（y﹣z）2+（x﹣y）2+（z﹣x）2=（y+z﹣2x）2+（z+x﹣2y）2+（x+y﹣2z）2．
求
的值．
【答案】1.
【解析】分析：利用等式的性質(zhì)將（y﹣z）2+（x﹣y）2+（z﹣x）2=（y+z﹣2x）2+（z+x﹣2y）2+（x+y﹣2z）2變形成（x﹣y）2+（x﹣z）2+（y﹣z）2=0的形式，從而得到x=y=z，再求得
的值.
詳解：
∵（y﹣z）2+（x﹣y）2+（z﹣x）2=（y+z﹣2x）2+（z+x﹣2y）2+（x+y﹣2z）2．
∴（y﹣z）2﹣（y+z﹣2x）2+（x﹣y）2﹣（x+y﹣2z）2+（z﹣x）2﹣（z+x﹣2y）2=0，
∴（y﹣z+y+z﹣2x）（y﹣z﹣y﹣z+2x）+（x﹣y+x+y﹣2z）（x﹣y﹣x﹣y+2z）+（z﹣x+z+x﹣2y）（z﹣x﹣z﹣x+2y）=0，
∴2x2+2y2+2z2﹣2xy﹣2xz﹣2yz=0，
∴（x﹣y）2+（x﹣z）2+（y﹣z）2=0．
∵x，y，z均為實數(shù)，
∴x=y=z．
∴=
=1．
開心快樂假期作業(yè)暑假作業(yè)西安出版社系列答案
名題訓(xùn)練系列答案
期末集結(jié)號系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦！ | 初一 | 初一免費(fèi)課程推薦！ |
| 高二 | 高二免費(fèi)課程推薦！ | 初二 | 初二免費(fèi)課程推薦！ |
| 高三 | 高三免費(fèi)課程推薦！ | 初三 | 初三免費(fèi)課程推薦！ |
科目：初中數(shù)學(xué) 來源： 題型：
【題目】若點(diǎn)（x1，y1），（x2，y2），（x3，y3）都是反比例函數(shù)y=﹣
圖象上的點(diǎn)，并且y1＜0＜y2＜y3，則下列各式中正確的是（ ）
A．x1＜x2＜x3 B．x1＜x3＜x2
C．x2＜x1＜x3 D．x2＜x3＜x1
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，在菱形ABCD中，AB=10，AC=16，點(diǎn)M是對角線AC上的一個動點(diǎn)，過點(diǎn)M作PQ⊥AC交AB于點(diǎn)P，交AD于點(diǎn)Q，將△APQ沿PQ折疊，點(diǎn)A落在點(diǎn)E處，當(dāng)△BCE是等腰三角形時，AP的長為_____．
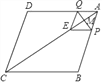
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】某科技有限公司準(zhǔn)備購進(jìn)A和B兩種機(jī)器人來搬運(yùn)化工材料，已知購進(jìn)A種機(jī)器人2個和B種機(jī)器人3個共需16萬元，購進(jìn)A種機(jī)器人3個和B種機(jī)器人2個共需14萬元，請解答下列問題：
（1）求A、B兩種機(jī)器人每個的進(jìn)價；
（2）已知該公司購買B種機(jī)器人的個數(shù)比購買A種機(jī)器人的個數(shù)的2倍多4個，如果需要購買A、B兩種機(jī)器人的總個數(shù)不少于28個，且該公司購買的A、B兩種機(jī)器人的總費(fèi)用不超過106萬元，那么該公司有哪幾種購買方案？
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】對于二次函數(shù)y=x2+mx+1，當(dāng)0＜x≤2時的函數(shù)值總是非負(fù)數(shù)，則實數(shù)m的取值范圍為（ ）
A. m≥﹣2 B. ﹣4≤m≤﹣2 C. m≥﹣4 D. m≤﹣4或m≥﹣2
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，數(shù)軸上A，B兩點(diǎn)對應(yīng)的有理數(shù)分別為10和15，點(diǎn)P從點(diǎn)A出發(fā)，以每秒1個單位長度的速度沿數(shù)軸正方向運(yùn)動，點(diǎn)Q同時從原點(diǎn)O出發(fā)，以每秒2個單位長度的速度沿數(shù)軸正方向運(yùn)動，設(shè)運(yùn)動時間為t秒．
(1)當(dāng)0＜t＜5時，用含t的式子填空：
BP＝_______，AQ＝_______；
(2)當(dāng)t＝2時，求PQ的值；
(3)當(dāng)PQ＝
AB時，求t的值．
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，在△ABC中，點(diǎn)D、E、F分別是邊AB、AC、BC的中點(diǎn)，要判定四邊形DBFE是菱形，下列所添加條件不正確的是（ ）
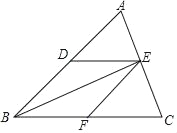
A. AB=AC B. AB=BC C. BE平分∠ABC D. EF=CF
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】（1）①觀察一列數(shù)1，2，3，4，5，…，發(fā)現(xiàn)從第二項開始，每一項與前一項之差是一個常數(shù)，這個常數(shù)是 ；根據(jù)此規(guī)律，如果
（
為正整數(shù)）表示這個數(shù)列的第項，那么
，
；
②如果欲求
的值，可令
……………①
將①式右邊順序倒置，得
……………②
由②加上①式，得2
；
∴ S=_________________；
由結(jié)論求
；
（2）①觀察一列數(shù)2，4，8，16，32，…，發(fā)現(xiàn)從第二項開始，每一項與前一項之比是一個常數(shù)，這個常數(shù)是 ；根據(jù)此規(guī)律，如果（為正整數(shù)）表示這個數(shù)列的第項，那么 ， ；
②為了求
的值，可令
，則
，因此
，所以
，
即
.
仿照以上推理，計算
查看答案和解析>>
科目：初中數(shù)學(xué) 來源： 題型：
【題目】如圖，一張矩形紙片
.點(diǎn)
在這張矩形紙片的邊
上，將紙片折疊，使
落在射線
上，折痕為
，點(diǎn)
分別落在點(diǎn)
處，
（1）若
，則
的度數(shù)為 °;
（2）若
,求
的長.
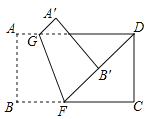
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com