
【題目】在平面直角坐標系![]() 中,拋物線
中,拋物線![]() 與
與![]() 軸交于點
軸交于點![]() ,其頂點記為
,其頂點記為![]() ,自變量
,自變量![]() 和
和![]() 對應的函數值相等.若點
對應的函數值相等.若點![]() 在直線
在直線![]() :
:![]() 上,點
上,點![]() 在拋物線上.
在拋物線上.
(1)求該拋物線的解析式;
(2)設![]() 對稱軸右側
對稱軸右側![]() 軸上方的圖象上任一點為
軸上方的圖象上任一點為![]() ,在
,在![]() 軸上有一點
軸上有一點![]() ,試比較銳角
,試比較銳角![]() 與
與![]() 的大小(不必證明),并寫出相應的
的大小(不必證明),并寫出相應的![]() 點橫坐標
點橫坐標![]() 的取值范圍;
的取值范圍;
(3)直線![]() 與拋物線另一點記為
與拋物線另一點記為![]() ,
,![]() 為線段
為線段![]() 上一動點(點
上一動點(點![]() 不與
不與![]() 重合).設
重合).設![]() 點坐標為
點坐標為![]() ,過
,過![]() 作
作![]()
![]() 軸于點
軸于點![]() ,將以點
,將以點![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形的面積
為頂點的四邊形的面積![]() 表示為
表示為![]() 的函數,標出自變量
的函數,標出自變量![]() 的取值范圍,并求出
的取值范圍,并求出![]() 可能取得的最大值.
可能取得的最大值.
【答案】(1)拋物線的解析式為y=4x2﹣16x+8;(2)當x=![]() 時,∠PCO=∠ACO,當2+
時,∠PCO=∠ACO,當2+![]() <x<
<x<![]() 時,∠PCO<∠ACO,當
時,∠PCO<∠ACO,當![]() <x<4時,∠PCO>∠ACO;(3)祥見解析.
<x<4時,∠PCO>∠ACO;(3)祥見解析.
【解析】
試題分析:(1)根據已知條件得到拋物線的對稱軸為x=2.設拋物線的解析式為y=a(x﹣2)2﹣8.將(3,﹣4)代入得拋物線的解析式為y=4(x﹣2)2﹣8,即可得到結論;
(2)由題意得:C(0,8),M(2,﹣8),如圖,當∠PCO=∠ACO時,過P作PH⊥y軸于H,設CP的延長線交x軸于D,則△ACD是等腰三角形,于是得到OD=OA=![]() ,根據相似三角形的性質得到x=
,根據相似三角形的性質得到x=![]() ,過C作CE∥x軸交拋物線與E,則CE=4,設拋物線與x軸交于F,B,則B(2+
,過C作CE∥x軸交拋物線與E,則CE=4,設拋物線與x軸交于F,B,則B(2+![]() ,0),于是得到結論;
,0),于是得到結論;
(3)解方程組得到D(﹣1,28得到Q(t,﹣12t+16)(﹣1≤t<2),①當﹣1≤t<0時,②當0<t<![]() 時,③當
時,③當![]() <t<2時,求得二次函數的解析式即可得到結論.
<t<2時,求得二次函數的解析式即可得到結論.
試題解析:(1)∵自變量x=﹣1和x=5對應的函數值相等,∴拋物線的對稱軸為x=2.
∵點M在直線l:y=﹣12x+16上,∴yM=﹣8.
設拋物線的解析式為y=a(x﹣2)2﹣8.將(3,﹣4)代入得:a﹣8=﹣4,解得:a=4.
∴拋物線的解析式為y=4(x﹣2)2﹣8,整理得:y=4x2﹣16x+8.
(2)由題意得:C(0,8),M(2,﹣8),
如圖,當∠PCO=∠ACO時,過P作PH⊥y軸于H,設CP的延長線交x軸于D,則△ACD是等腰三角形,
∴OD=OA=![]() ,∵P點的橫坐標是x,∴P點的縱坐標為4x2﹣16x+8,
,∵P點的橫坐標是x,∴P點的縱坐標為4x2﹣16x+8,
∵PH∥OD,∴△CHP∽△COD,∴![]() ,∴x=
,∴x=![]() ,
,
過C作CE∥x軸交拋物線與E,則CE=4,
設拋物線與x軸交于F,B,則B(2+![]() ,0),∴y=ax2+bx+c對稱軸右側x軸上方的圖象上任一點為P,
,0),∴y=ax2+bx+c對稱軸右側x軸上方的圖象上任一點為P,
∴當x=![]() 時,∠PCO=∠ACO,
時,∠PCO=∠ACO,
當2+![]() <x<
<x<![]() 時,∠PCO<∠ACO,
時,∠PCO<∠ACO,
當![]() <x<4時,∠PCO>∠ACO;
<x<4時,∠PCO>∠ACO;
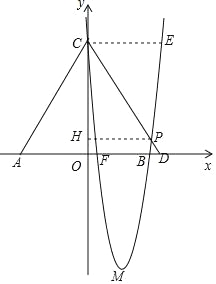
(3)解方程組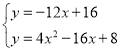 ,解得:
,解得:![]() ,∴D(﹣1,28),
,∴D(﹣1,28),
∵Q為線段BM上一動點(點Q不與M重合),∴Q(t,﹣12t+16)(﹣1≤t<2),
①當﹣1≤t<0時,S=![]() (﹣t)(﹣12t+16﹣8)+8(﹣t)=6t2﹣12t=6(t﹣1)2﹣6,
(﹣t)(﹣12t+16﹣8)+8(﹣t)=6t2﹣12t=6(t﹣1)2﹣6,
∵﹣1≤t<0,∴當t=-1時,S最大=18;
②當0<t<![]() 時,S=
時,S=![]() t8+
t8+![]() t(﹣12t+16)=﹣6t2+12t=﹣6(t﹣1)2+6,
t(﹣12t+16)=﹣6t2+12t=﹣6(t﹣1)2+6,
∵0<t<![]() ,∴當t=1時,S最大=6;
,∴當t=1時,S最大=6;
③當![]() <t<2時,S=
<t<2時,S=![]() t8+
t8+![]() (12t﹣16)=6t2﹣4t=6(t﹣
(12t﹣16)=6t2﹣4t=6(t﹣![]() )2﹣
)2﹣![]() ,
,
∵![]() <t<2,∴此時S=16為最大值.
<t<2,∴此時S=16為最大值.


科目:初中數學 來源: 題型:
【題目】有長為2cm、3cm、4cm、6cm的四根木棒,選其中的3根作為三角形的邊,可以圍成的三角形的個數是( )
A. 1個B. 2個C. 3個D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知反比例函數![]() (
(![]() 為常數).
為常數).
(1)若點![]() 和點
和點![]() 是該反比例函數圖象上的兩點,試利用反比例函數的性質比較
是該反比例函數圖象上的兩點,試利用反比例函數的性質比較![]() 和
和![]() 的大小;
的大小;
(2)設點![]() (
(![]() )是其圖象上的一點,過點
)是其圖象上的一點,過點![]() 作
作![]() 軸于點
軸于點![]() ,若
,若![]() ,
,![]() (
(![]() 為坐標原點),求
為坐標原點),求![]() 的值,并直接寫出不等式
的值,并直接寫出不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】氣候宜人的省級度假勝地吳川吉兆,測得一至五月份的平均氣溫分別為17、17、20、22、24(單位:℃),這組數據的中位數是( )
A.24
B.22
C.20
D.17
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,E、F是ABCD對角線AC上兩點,且AE=CF. 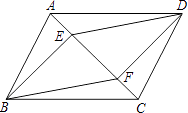
(1)求證:四邊形BFDE是平行四邊形.
(2)如果把條件AE=CF改為BE⊥AC,DF⊥AC,試問四邊形BFDE是平行四邊形嗎?為什么?
(3)如果把條件AE=CF改為BE=DF,試問四邊形BFDE還是平行四邊形嗎?為什么?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com