【題目】在平面直角坐標系中，任意兩點A（
， 
），B（
， 
），規定運算：①A⊕B=（
， 
）；②AB=
；③當
且
時，A=B，有下列四個命題：（1）若A（1，2），B（2，﹣1），則A⊕B=（3，1），AB=0；
（2）若A⊕B=B⊕C，則A=C；
（3）若AB=BC，則A=C；
（4）對任意點A、B、C，均有（A⊕B）⊕C=A⊕（B⊕C）成立，其中正確命題的個數為（ ）
A. 1個 B. 2個 C. 3個 D. 4個
科目：初中數學 來源： 題型：
【題目】已知函數y=﹣x+4，回答下列問題：
（1）請在右圖的直角坐標系中畫出函數y=﹣x+4圖象；
（2）y的值隨x值的增大而________；
（3）當y=2時，x的值為_________；
（4）當y＜0時，x的取值范圍是_______．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某校為了解初中學生每天在校體育活動的時間（單位：h），隨機調査了該校的部分初中學生．根據調查結果，繪制出如下的統計圖①和圖②．請根據相關信息，解答下列問題：
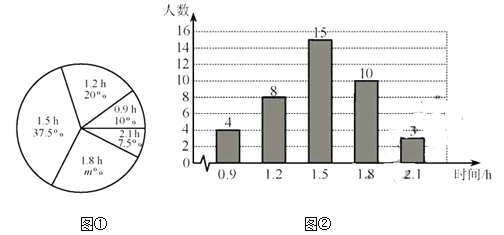
（Ⅰ）本次接受調查的初中學生人數為___________，圖①中m的值為_____________；
（Ⅱ）求統計的這組每天在校體育活動時間數據的平均數、眾數和中位數；
（Ⅲ）根據統計的這組每天在校體育活動時間的樣本數據，若該校共有800名初中學生，估計該校每天在校體育活動時間大于1h的學生人數．
查看答案和解析>>
科目：初中數學 來源： 題型：
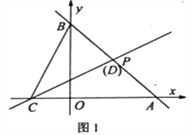
【題目】如圖，直線l1經過過點P（2，2），分別交x軸、y軸于點A（4，0），B。
（1）求直線l1的解析式；
（2）點C為x軸負半軸上一點，過點C的直線l2：
交線段AB于點D。
如圖1，當點D恰與點P重合時，點Q（t，0）為x軸上一動點，過點Q作QM⊥x軸，分別交直線l1、l2于點M、N。若
，MN=2MQ，求t的值；
如圖2，若BC=CD，試判斷m，n之間的數量關系并說明理由。
查看答案和解析>>
科目：初中數學 來源： 題型：
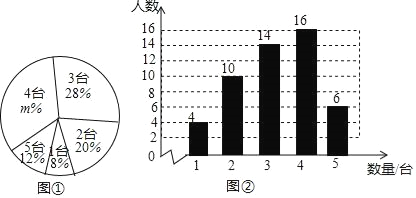
【題目】隨著移動計算技術和無線網絡的快速發展，移動學習方式越來越引起人們的關注，某校計劃將這種學習方式應用到教育學中，從全校1500名學生中隨機抽取了部分學生，對其家庭中擁有的移動設備的情況進行調查，并繪制出如下的統計圖①和圖②，根據相關信息，解答下列問題：
（1）本次接受隨機抽樣調查的學生人數為 ，圖①中m的值為 ；
（2）求本次調查獲取的樣本數據的眾數、中位數和平均數；
（3）根據樣本數據，估計該校1500名學生家庭中擁有3臺移動設備的學生人數．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，數軸上有三個點A、B、C，表示的數分別是﹣4、﹣2、3，請回答：
（1）若使C、B兩點的距離與A、B兩點的距離相等，則需將點C向左移動 個單位；
（2）若移動A、B、C三點中的兩個點，使三個點表示的數相同，移動方法有 種，其中移動所走的距離和最小的是 個單位；
（3）若在原點處有一只小青蛙，一步跳1個單位長．小青蛙第1次先向左跳1步，第2次再向右跳3步，然后第3次再向左跳5步，第4次再向右跳7步，…，按此規律繼續跳下去，那么跳第100次時，應跳 步，落腳點表示的數是 ；
（4）若有兩只小青蛙A、B，它們在數軸上的點表示的數分別為整數x、y，且|x﹣2|+|y+3|=2，求兩只小青蛙A、B之間的距離．
查看答案和解析>>
科目：初中數學 來源： 題型：
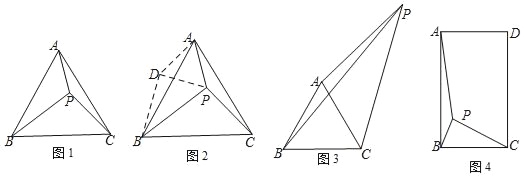
【題目】問題情境：如圖1，在等邊△ABC中，點P在△ABC內，且PA=3，PB=5，PC=4，求∠APC的度數？
小明在解決這個問題時，想到了以下思路：如圖2，把△APC繞著點A順時針旋轉，使點C旋轉到點B，得到△ADB，連結DP．
請你在小明的思路提示下，求出∠APC的度數．
思路應用：如圖3，△ABC為等邊三角形，點P在△ABC外，且PA=6，PC=8，∠APC=30°，求PB的長；
思路拓展：如圖4，矩形ABCD中，AB=
BC，P為矩形ABCD內一點，PA：PB：PC=2
：1：2，則∠APB= °．（直接填空）
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
