【題目】古希臘著名的畢達哥拉斯學派把1、3、6、10…這樣的數稱為“三角形數”，而把l、4、9、16…這樣的數稱為“正方形數”．從圖中可以發現，任何一個大于1的正方形數”都可以看作兩個相鄰“三角形數”之和．下列等式中。符合這一規律的是( )
A. 15＝4+11 B. 25＝9+16
C. 49＝21+28 D. 61＝25+36
【答案】C
【解析】∵1=1，1+2=3，1+2+3=6，1+2+3+4=10，…，
∴“三角形數”可看成從1開始幾個連續自然數的和；
∵1=12,4=22,9=32,16=42，…，
∴“正方形數”可看成某個自然數的平方。
A.∵在15=4+11中，15不是“正方形數”，且3、10不是兩個相鄰“三角形數”，
∴A選項不符合題意；
B.∵在25=9+16中，9、16、25是相鄰的三個“正方形數”，
∴B選項不符合題意；
C.∵1+2+3+4+5+6=21，1+2+3+4+5+6+7=28，
∴21、28是兩個相鄰“三角形數”，
∵49=72，
∴49是“正方形數”，
C選項符合題意；
D.∵在61＝25+36中，61不是“正方形數”，
∴D選項不符合題意。
故選C.
科目：初中數學 來源： 題型：
【題目】甲、乙兩工程隊維修同一段路面，甲隊先清理路面，乙隊在甲隊清理后鋪設路面．乙隊在中途停工了一段時間，然后按停工前的工作效率繼續工作．在整個工作過程中，甲隊清理完的路面長y（米）與時間x（時）的函數圖象為線段OA，乙隊鋪設完的路面長y（米）與時間x（時）的函數圖象為折線BC-CD-DE，如圖所示，從甲隊開始工作時計時．
（1）分別求線段BC、DE所在直線對應的函數關系式．
（2）當甲隊清理完路面時，求乙隊鋪設完的路面長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖Ⅰ，在第四象限的矩形ABCD，點A與坐標原點O重合，且AB=4，AD=3.如圖Ⅱ，矩形ABCD沿OC方向以每秒1個單位長度的速度運動，同時點Q從B點出發也以每秒1個單位長度的速度沿矩形ABCD的邊BC經過點C向點D運動，當點Q到達點D時，矩形ABCD和點Q同時停止運動，設點Q運動的時間為t秒.
（1）在圖Ⅰ中，點C的坐標(____),在圖Ⅱ中，當t=2時，點A坐標(______),Q坐標(______)
（2）當點Q在線段BC或線段CD上運動時，求出△ACQ的面積S關于t的函數關系式，并寫出t的取值范圍;
（3）點Q在線段BC或線段CD上運動時，作QM⊥x軸，垂足為點M，當△QMO與△ACD相似時，求出相應的t值.
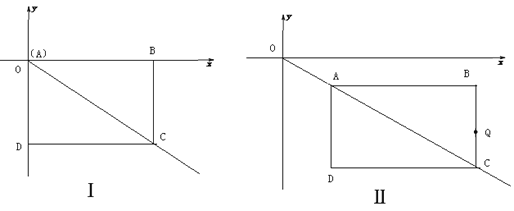
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在正方形網格中，△TAB頂點坐標分別為T(1，1)、A(2，3)、B(4，2)．
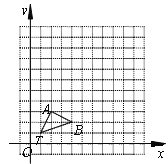
(1)以點T（1，1）為位似中心，按比例尺（TA′∶TA）3∶1在位似中心的同側將△TAB放大為△TA′B′，放大后點A、B的對應點分別為A′、B′．畫出△TA′B′，并寫出點A′、B′的坐標；
(2)在（1）中，若C（a，b）為線段AB上任一點，寫出變化后點C的對應點C′的坐標．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，△ABC的中線BE與CD交于點G，連接DE，下列結論不正確的是（ ）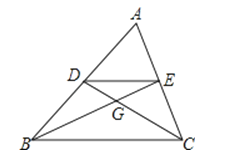
A.點G是△ABC的重心
B.DE∥BC
C.△ABC的面積=2△ADE的面積
D.BG=2GE
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖①，AB是⊙O的一條弦，點C是優弧
上一點．
（1）若∠ACB=45°，點P是⊙O上一點（不與A、B重合），則∠APB= ；
（2）如圖②，若點P是弦AB與所圍成的弓形區域（不含弦AB與）內一點．求證：∠APB＞∠ACB；
（3）請在圖③中直接用陰影部分表示出在弦AB與所圍成的弓形區域內滿足∠ACB＜∠APB＜2∠ACB的點P所在的范圍．
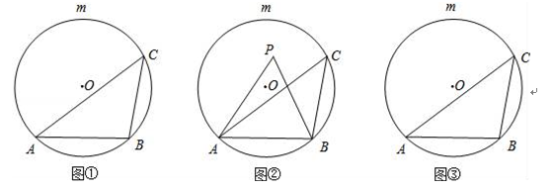
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com