
【題目】計算與解方程
(1)計算: ![]() ﹣3×(﹣2)2;
﹣3×(﹣2)2;
(2)用公式法解:x2﹣3x﹣1=0.
【答案】
(1)解:原式=2﹣3×4=2﹣12=﹣10
(2)解:∵a=1,b=﹣3,c=﹣1,
∴b2﹣4ac=9+4=13>0,
∴x= ![]() ,
,
即x1= ![]() ,x2=
,x2= ![]()
【解析】(1)先計算乘方和根號,再計算乘法,最后計算加減即可;(2)公式法求解可得.
【考點精析】解答此題的關鍵在于理解二次根式的性質與化簡的相關知識,掌握1、如果被開方數是分數(包括小數)或分式,先利用商的算數平方根的性質把它寫成分式的形式,然后利用分母有理化進行化簡.2、如果被開方數是整數或整式,先將他們分解因數或因式,然后把能開得盡方的因數或因式開出來,以及對公式法的理解,了解要用公式解方程,首先化成一般式.調整系數隨其后,使其成為最簡比.確定參數abc,計算方程判別式.判別式值與零比,有無實根便得知.有實根可套公式,沒有實根要告之.


 同步練習西南大學出版社系列答案
同步練習西南大學出版社系列答案 補充習題江蘇系列答案
補充習題江蘇系列答案 學練快車道口算心算速算天天練系列答案
學練快車道口算心算速算天天練系列答案科目:初中數學 來源: 題型:
【題目】某校八年級同學到距學校6km的郊外游玩,一部分同學步行,另一部分同學騎車。如圖, ![]() 分別表示步行和騎車的同學前往目的地所走的路程y(km)與所用的時間x(min)之間的函數圖像,則下列判斷錯誤的是
分別表示步行和騎車的同學前往目的地所走的路程y(km)與所用的時間x(min)之間的函數圖像,則下列判斷錯誤的是

A. 騎車的同學比步行的同學晚出發30min
B. 步行的同學的速度是6km/h
C. 騎車的同學從出發到追上步行的同學用了20min
D. 騎車的同學和步行的同學同時到達目的地
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,已知△ABC的三個頂點的坐標分別為A(﹣3,5),B(﹣2,1),C(﹣1,3). 
①若△ABC經過平移后得到△A1B1C1 , 已知點C1的坐標為(4,0),寫出頂點A1 , B1的坐標;
②若△ABC和△A2B2C2關于原點O成中心對稱圖形,寫出△A2B2C2的各頂點的坐標;
③將△ABC繞著點O按順時針方向旋轉90°得到△A3B3C3 , 寫出△A3B3C3的各頂點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于一次函數y=x+6,下列結論錯誤的是( )
A. 函數值隨自變量增大而增大 B. 函數圖像與![]() 軸正方向成45°角
軸正方向成45°角
C. 函數圖像不經過第四象限 D. 函數圖像與![]() 軸交點坐標是(0,6)
軸交點坐標是(0,6)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,OABC是一張放在平面直角坐標系中的矩形紙片,O為原點,點A在x軸的正半軸上,點C在y軸的正半軸上,OA=10,OC=8,在OC邊上取一點D,將紙片沿AD翻折,使點O落在BC邊上的點E處,則D點的坐標是 .
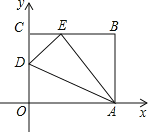
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,已知AB是圓O的直徑,圓O過BC的中點D,且DE⊥AC. 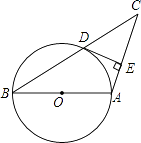
(1)求證:DE是圓O的切線;
(2)若∠C=30°,CD=10cm,求圓O的半徑.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com