
【題目】近日,深圳市人民政府發布了《深圳市可持續發展規劃》,提出了要做可持續發展的全球創新城市的目標,某初中學校了解學生的創新意識,組織了全校學生參加創新能力大賽,從中抽取了部分學生成績,分為5組:A組50~60;B組60~70;C組70~80;D組80~90;E組90~100,統計后得到如圖所示的頻數分布直方圖(每組含最小值不含最大值)和扇形統計圖.
(1)抽取學生的總人數是 人,扇形C的圓心角是 °;
(2)補全頻數直方圖;
(3)該校共有2200名學生,若成績在70分以下(不含70分)的學生創新意識不強,有待進一步培養,則該校創新意識不強的學生約有多少人?
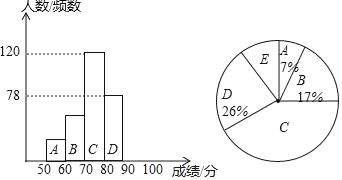
【答案】(1)300、144;(2)補全頻數分布直方圖見解析;(3)該校創新意識不強的學生約有528人.
【解析】
(1)由D組頻數及其所占比例可得總人數,用360°乘以C組人數所占比例可得;
(2)用總人數分別乘以A、B組的百分比求得其人數,再用總人數減去A、B、C、D的人數求得E組的人數可得;
(3)用總人數乘以樣本中A、B組的百分比之和可得.
解:(1)抽取學生的總人數為78÷26%=300人,扇形C的圓心角是360°×![]() =144°,
=144°,
故答案為:300、144;
(2)A組人數為300×7%=21人,B組人數為300×17%=51人,
則E組人數為300﹣(21+51+120+78)=30人,
補全頻數分布直方圖如下:
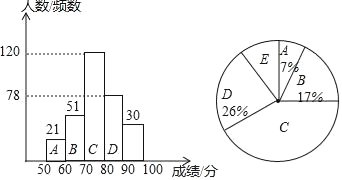
(3)該校創新意識不強的學生約有2200×(7%+17%)=528人.


科目:初中數學 來源: 題型:
【題目】舉世矚目的港珠澳大橋已于2018年10月24日正式通車,這座大橋是世界上最長的跨海大橋,被英國《衛報》譽為“新世界七大奇跡”,車輛經過這座大橋收費站時,從已開放的4個收費通道A、B、C、D中可隨機選擇其中一個通過.
(1)一輛車經過收費站時,選擇A通道通過的概率是 .
(2)用樹狀圖或列表法求兩輛車經過此收費站時,選擇不同通道通過的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(10分)學校組織學生參加綜合實踐活動,他們參與了某種品牌運動鞋的銷售工作,已知該運動鞋每雙的進價為120元,為尋求合適的銷售價格進行了4天的試銷,試銷情況如下表所示:
第1天 | 第2天 | 第3天 | 第4天 | |
售價x(元/雙) | 150 | 200 | 250 | 300 |
銷售量y(雙) | 40 | 30 | 24 | 20 |
(1)觀察表中數據,x,y滿足什么函數關系?請求出這個函數關系式;
(2)若商場計劃每天的銷售利潤為3000元,則其單價定為多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】“勤勞”是中華民族的傳統美德,學校要求同學們在家里幫助父母做些力所能及的家務.王剛同學在本學期開學初對部分同學寒假在家做家務的時間進行了抽樣調查(時間取整數小時),所得數據統計如下表:
時間分組 | 0.5~20.5 | 20.5~40.5 | 40.5~60.5 | 60.5~80.5 | 80.5~100.5 |
頻 數 | 20 | 25 | 30 | 15 | 10 |
(1)抽取樣本的容量是 .
(2)根據表中數據補全圖中的頻數分布直方圖
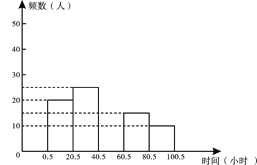
(3)樣本的中位數所在時間段的范圍是 .
(4)若該學校有學生1260人,那么大約有多少學生在寒假做家務的時間在40.5~100.5小時之間?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,⊙O交x軸于A、B兩點,直線FA⊥x軸于點A,點D在FA上,且DO平行于⊙O的弦MB,連接DM并延長交x軸于點C.
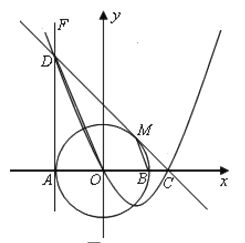
(1)判斷直線DC與⊙O的位置關系,并給出證明;
(2)設點D的坐標為(-2,4),試求經過D、O、C三點的拋物線的解析式.
(3)若坐標平面內的點P,使得以點P和三點D、O、C為頂點的四邊形是平行四邊形,求P點的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中有兩點![]() ,若二次函數
,若二次函數![]() 的圖像與線段AB只有一個交點,則( )
的圖像與線段AB只有一個交點,則( )
A.![]() 的值可以是
的值可以是![]() B.
B.![]() 的值可以是
的值可以是![]()
C.![]() 的值不可能是-1.2D.
的值不可能是-1.2D.![]() 的值不可能是-1
的值不可能是-1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線![]() (
(![]() 為常數)與雙曲線
為常數)與雙曲線![]() (
(![]() 為常數)相交于
為常數)相交于![]() 、
、![]() 兩點.
兩點.
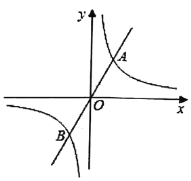
(1)若點![]() 的橫坐標為3,點
的橫坐標為3,點![]() 的縱坐標為
的縱坐標為![]() .直接寫出:
.直接寫出:![]() ________,
________,![]() _______,
_______,![]() 的解集為_______.
的解集為_______.
(2)若雙曲線![]() (
(![]() 為常數)的圖象上有點
為常數)的圖象上有點![]() ,
,![]() ,當
,當![]() 時,比較
時,比較![]() 與
與![]() 的大小.
的大小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,某人為了測量小山頂上的塔ED的高,他在山下的點A處測得塔尖點D的仰角為45°,再沿AC方向前進60 m到達山腳點B,測得塔尖點D的仰角為60°,塔底點E的仰角為30°,求塔ED的高度.(結果保留根號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】一個不透明的口袋里裝有分別標有漢字“美”、“麗”、“光”、“明”的四個小球,除漢字不同之外,小球沒有任何區別,每次摸球前先攪拌均勻再摸球.
(1)若從中任取一個球,求摸出球上的漢字剛好是“美”的概率;
(2)甲從中任取一球,不放回,再從中任取一球,請用樹狀圖或列表法,求甲取出的兩個球上的漢字恰能組成“美麗”或“光明”的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com