
【題目】我們知道1+2+3+…+![]() =
=![]() ,則1+2+3+…+10= ___________ .
,則1+2+3+…+10= ___________ .
[問題提出] 那么 ![]() 的結果等于多少呢?
的結果等于多少呢?
[閱讀理解] 在圖1所示的三角形數陣中,第1行圓圈中的數為1,即12 ;第2行兩個圓圈中數的和為2+2,即22;......;第n行n個圓圈中數的和為n+n+![]() n即 n2;這樣,該三角形數陣中共有____ 個圓圈,所有圓圈中數的和可表示為_________________ .
n即 n2;這樣,該三角形數陣中共有____ 個圓圈,所有圓圈中數的和可表示為_________________ .
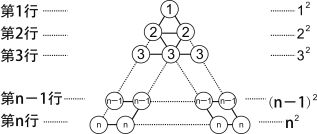
圖1
[規律探究] 將三角形數陣經兩次旋轉可得如圖2所示的三角形數陣,觀察這三個三角形數陣各行同一位置圓圈中的數(如第n-1行的第一個圓圈中的數分別為n-1,2,n)發現每個位置上三個圓圈中的數的和均為______________.由此可得,這三個三角形數陣所有圓圈中數的總和為:
3(![]() )=_________________.因此,
)=_________________.因此,![]() =__________.
=__________.

圖2
[問題解決]
(1).根據以上規律可得![]() __________________.
__________________.
(2).試計算 ![]() ,請寫出計算步驟.
,請寫出計算步驟.
【答案】55;![]() ;
;![]() ;(
;(![]() );
);![]() ;
;![]() ;(1)7;(2)2485
;(1)7;(2)2485
【解析】
把n=10代入1+2+3+…+![]() =
=![]() ,即可求出1+2+3+…+10的值;
,即可求出1+2+3+…+10的值;
[閱讀理解]:由圖1可知,共有1+2+3+…+n=![]() 個圓圈,所有圓圈中數的和可表示為
個圓圈,所有圓圈中數的和可表示為![]() ;
;
[規律探究]:由圖2知,每個位置上三個圓圈中的數的和均為![]() .由此可得,這三個三角形數陣所有圓圈中數的總和為:3(
.由此可得,這三個三角形數陣所有圓圈中數的總和為:3(![]() )=每個位置上三個圓圈中的數的和(
)=每個位置上三個圓圈中的數的和(![]() )×位置的個數
)×位置的個數![]() ,因此,
,因此,![]() =
=![]() ;
;
[問題解決]:(1)先化簡把![]() ,然后把n=10代入就算即可;(2)用(
,然后把n=10代入就算即可;(2)用(![]() )減去(
)減去(![]() )即可求出結論.
)即可求出結論.
當n=10時,
1+2+3+…+![]() =
=![]() =55;
=55;
[閱讀理解]:由圖1可知,共有1+2+3+…+n=![]() 個圓圈,所有圓圈中數的和可表示為
個圓圈,所有圓圈中數的和可表示為![]() ;
;
[規律探究]:由圖2知,每個位置上三個圓圈中的數的和均為![]() .由此可得,這三個三角形數陣所有圓圈中數的總和為:3(
.由此可得,這三個三角形數陣所有圓圈中數的總和為:3(![]() )=
)=![]() ,因此,
,因此,![]() =
=![]() ;
;
[問題解決]:(1)∵![]() ,
,
把n=10代入得,
原式=![]() =7;
=7;
(2)![]()
=(![]() )-(
)-(![]() )
)
=![]()
=![]()
=2485.


科目:初中數學 來源: 題型:
【題目】有一多邊形草坪,在市政建設設計圖紙上的面積為300cm2,其中一條邊的長度為5cm.經測量,這條邊的實際長度為15m,則這塊草坪的實際面積是( )
A. 100m2 B. 270m2 C. 2700m2 D. 90000m2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某中學庫存一批舊桌凳,準備修理后捐助貧困山區學校.現有甲、乙兩個木工小組都想承攬這項業務,經協商得知:甲小組單獨修理這批桌凳比乙小組多用20天,乙小組每天比甲小組多修8套,甲小組每天修16套桌凳;學校每天需付甲小組修理費80元,付乙小組120元.
(1)求甲、乙兩個木工小組單獨修理這批桌凳各需多少天.
(2)在修理桌凳的過程中,學校要委派一名維修工進行質量監督,并由學校負擔他每天10元的生活補助.現有下面三種修理方案供選擇:
①由甲小組單獨修理;②由乙小組單獨修理;③由甲、乙兩小組合作修理.
你認為哪種方案既省時又省錢?試比較說明.
查看答案和解析>>
科目:初中數學 來源: 題型:
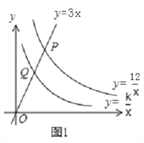
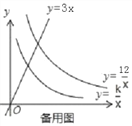
【題目】如圖1,已知直線y=3x分別與雙曲線y=![]() 、y=
、y=![]() (x>0)交于P、Q兩點,且OP=2OQ.
(x>0)交于P、Q兩點,且OP=2OQ.
(1)求k的值.
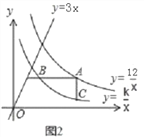
(2)如圖2,若點A是雙曲線y= ![]() 上的動點,AB∥x軸,AC∥y軸,分別交雙曲線y=
上的動點,AB∥x軸,AC∥y軸,分別交雙曲線y=![]() (x>0)于點B、C,連接BC.請你探索在點A運動過程中,△ABC的面積是否變化?若不變,請求出△ABC的面積;若改變,請說明理由;
(x>0)于點B、C,連接BC.請你探索在點A運動過程中,△ABC的面積是否變化?若不變,請求出△ABC的面積;若改變,請說明理由;
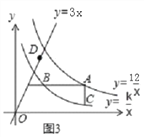
(3)如圖3,若點D是直線y=3x上的一點,請你進一步探索在點A運動過程中,以點A、B、C、D為頂點的四邊形能否為平行四邊形?若能,求出此時點A的坐標;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某工廠一周計劃每日生產某產品100噸,由于工人實行輪休,每日上班人數不一定相等,實際每日生產量與計劃量相比情況如下表(以計劃量為標準,增加的噸數記為正數,減少的噸數記為負數)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增減/噸 | ﹣1 | +3 | ﹣2 | +4 | +7 | ﹣5 | ﹣10 |
(1)生產量最多的一天比生產量最少的一天多生產多少噸?
(2)本周總生產量是多少噸?比原計劃增加了還是減少了?增減數為多少噸?
(3)若本周總生產的產品全部由35輛貨車一次性裝載運輸離開工廠,則平均每輛貨車大約需裝載多少噸?(結果精確到0.01噸)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 兩地盛產柑桔,
兩地盛產柑桔,![]() 地有柑桔200噸,
地有柑桔200噸,![]() 地有柑桔300噸.現將這些柑桔運到C、D兩個冷藏倉庫,已知
地有柑桔300噸.現將這些柑桔運到C、D兩個冷藏倉庫,已知![]() 倉庫可儲存240噸,
倉庫可儲存240噸,![]() 倉庫可儲存260噸;從
倉庫可儲存260噸;從![]() 地運往C、D兩處的費用分別為每噸20元和25元,從
地運往C、D兩處的費用分別為每噸20元和25元,從![]() 地運往C、D兩處的費用分別為每噸15元和18元.設從
地運往C、D兩處的費用分別為每噸15元和18元.設從![]() 地運往
地運往![]() 倉庫的柑桔重量為x噸,A、B兩地運往兩倉庫的柑桔運輸費用分別為yA元和yB元.
倉庫的柑桔重量為x噸,A、B兩地運往兩倉庫的柑桔運輸費用分別為yA元和yB元.
(1)請填寫下表后分別求出yA,yB之間的函數關系式,并寫出定義域;
| C | D | 總計 |
A | x噸 | 200噸 | |
B | 300噸 | ||
總計 | 240噸 | 260噸 | 500噸 |
(2)試討論A,B兩地中,哪個運費較少;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,點A的坐標是(0,3),點B在x軸上,將△AOB繞點A逆時針旋轉90°得到△AEF,點O、B的對應點分別是點E、F.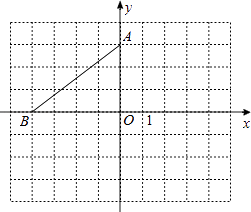
(1)若點B的坐標是(﹣4,0),請在圖中畫出△AEF,并寫出點E、F的坐標.
(2)當點F落在x軸的上方時,試寫出一個符合條件的點B的坐標.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】觀察下面三行數:
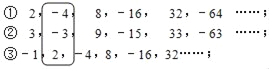
取每一行的第n個數,依次記為x、y、z.如上圖中,當n=2時,x=﹣4,y=﹣3,z=2.
(1)當n=7時,請直接寫出x、y、z的值,并求這三個數中最大的數與最小的數的差;
(2)已知n為偶數,且x、y、z這三個數中最大的數與最小的數的差為384,求n的值;
(3)若m=x+y+z,則x、y、z這三個數中最大的數與最小的數的差為 (用含m的式子表示)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法中錯誤的有( )個
①絕對值相等的兩數相等.②若a,b互為相反數,則![]() =﹣1.③如果a大于b,那么a的倒數小于b的倒數.④任意有理數都可以用數軸上的點來表示.⑤x2﹣2x﹣33x3+25是五次四項.⑥兩個負數比較大小,絕對值大的反而小.⑦一個數的相反數一定小于或等于這個數.⑧正數的任何次冪都是正數,負數的任何次冪都是負數.
=﹣1.③如果a大于b,那么a的倒數小于b的倒數.④任意有理數都可以用數軸上的點來表示.⑤x2﹣2x﹣33x3+25是五次四項.⑥兩個負數比較大小,絕對值大的反而小.⑦一個數的相反數一定小于或等于這個數.⑧正數的任何次冪都是正數,負數的任何次冪都是負數.
A. 4個 B. 5個 C. 6個 D. 7個
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com