
【題目】正方形ABCD中,點M是直線BC上的一個動點(不與點B,C重合),作射線DM,過點B作BN⊥DM于點N,連接CN.
(1)如圖1,當點M在BC上時,如果∠CDM=25°,那么∠MBN的度數是 .
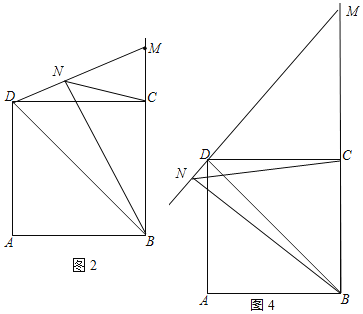
(2)如圖2,當點M在BC的延長線上時,
①依題意補全圖2;
②用等式表示線段NB,NC和ND之間的數量關系,并證明.

【答案】(1)![]() ;(2)①見解析;②
;(2)①見解析;②![]() ,見解析.
,見解析.
【解析】
(1)由正方形的性質和對頂角相等、三角形內角和定理得出∠MBN=∠CDM=25°即可;
(2)①由題意補全圖形即可;
②當N在DM上時,在NB上截取BE=ND,證明△CDN≌△CBE得出NC=EC,∠DCN=∠BCE,證出∠NCE=∠BCD=90°,得出△NCE是等腰直角三角形,得出NE=![]() NC,即可得出結論;
NC,即可得出結論;
當N在MD延長線上時,延長NB至E,使BE=ND,同理得:△CDN≌△CBE,得出NC=EC,∠DCN=∠BCE,證出∠NCE=∠BCD=90°,得出△NCE是等腰直角三角形,證出NE=![]() NC,即可得出結論.
NC,即可得出結論.
解:(1)∵四邊形ABCD是正方形,
∴BC=CD,∠DCM=∠BCD=90°,
∵BN⊥DM,
∴∠DNB=90°=∠BCD,
∵∠BMN=∠DMC,
∴∠MBN=∠CDM=25°;
故答案為:25°;
(2)①由題意補全圖形如圖2、圖4所示;
②線段NB,NC和ND之間的數量關系為:NB=ND+![]() NC,或
NC,或![]() NC=NB+ND.
NC=NB+ND.
理由如下:
當N在DM上時,在NB上截取BE=ND,

∵∠MCD=∠BNM=90°,
∴∠DMC+∠CDN=∠DMC+∠CBE=90°,
∴∠CDN=∠CBE,
在△CDN和△CBE中,
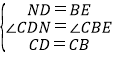 ,
,
∴△CDN≌△CBE(SAS),
∴NC=EC,∠DCN=∠BCE,
∴∠NCE=∠DCN+∠DCE=∠BCE+∠DCE=∠BCD=90°,
∴△NCE是等腰直角三角形,
∴NE=![]() NC,
NC,
∴NB=BE+NE=ND+![]() NC;
NC;
當N在MD延長線上時,延長NB至E,使BE=ND,

同理得:△CDN≌△CBE,
∴NC=EC,∠DCN=∠BCE,
∴∠NCE=∠DCN+∠DCE=∠BCE+∠DCE=∠BCD=90°,
∴△NCE是等腰直角三角形,
∴NE=![]() NC,
NC,
∵NE=NB+BE,
∴![]() NC=NB+ND.
NC=NB+ND.


科目:初中數學 來源: 題型:
【題目】簡答題:
(1)當![]() 為何值時,關于
為何值時,關于![]() 的方程
的方程![]() 是一元二次方程?
是一元二次方程?
(2)已知關于![]() 的一元二次方程
的一元二次方程![]() 有一個根是0,求
有一個根是0,求![]() 的值.
的值.
(3)在第(2)題中,如果要使已知方程有一個根是l,那么m應該等于什么數?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】天空中有一個靜止的廣告氣球C,從地面A點測得C點的仰角為45°,從地面B測得仰角為60°,已知AB=20米,點C和直線AB在同一鉛垂平面上,求氣球離地面的高度.(結果精確到0.1米)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,在直角梯形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .動點
.動點![]() 從點
從點![]() 出發,沿邊
出發,沿邊![]() 向點
向點![]() 以每秒2個單位長的速度運動,動點
以每秒2個單位長的速度運動,動點![]() 同時從點
同時從點![]() 出發,在邊
出發,在邊![]() 上以每秒1個單位長的速度向點
上以每秒1個單位長的速度向點![]() 運動,當其中一個動點到達端點時另一個動點也隨之停止運動.設運動的時間為
運動,當其中一個動點到達端點時另一個動點也隨之停止運動.設運動的時間為![]() (秒),
(秒),
(1)①設![]() 的面積為
的面積為![]() ,求
,求![]() 與
與![]() 之間的函數關系式,并寫出自變量
之間的函數關系式,并寫出自變量![]() 的取值范圍;
的取值范圍;
②當![]() 為何值時,
為何值時,![]() ?
?![]() 能不能等于
能不能等于![]() ?為什么?
?為什么?
(2)①當![]() 為何值時,
為何值時,![]() ?
?
②當![]() 為何值時,點
為何值時,點![]() 是在
是在![]() 的垂直平分線上?
的垂直平分線上?
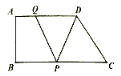
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)如圖1,![]() 為正方形
為正方形![]() 的邊
的邊![]() 上一點,將正方形
上一點,將正方形![]() 沿
沿![]() 折疊,點
折疊,點![]() 落在點
落在點![]() 處,連接并延長
處,連接并延長![]() ,交
,交![]() 于點
于點![]() ,求證:
,求證:![]() ;
;
(2)如圖2,點![]() 分別在
分別在![]() 邊上,且
邊上,且![]() ,求證:
,求證:![]()
(3)如圖3,點![]() 分別在
分別在![]() 邊上,點
邊上,點![]() 分別在
分別在![]() 邊上,
邊上,![]() 交
交![]() 于點
于點![]() ,已知
,已知![]() ,
,![]() ,
,![]() ,求
,求![]() 的長.
的長.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某服裝店購進一批甲、乙兩種款型襯衫,甲種款型共用了7800元,乙種款型共用了6400元,甲種款型的件數是乙種款型件數的1.5倍,甲種款型每件的進價比乙種款型每件的進價少30元.
(1)求甲、乙兩種款型的襯衫各購進多少件?
(2)商店進價提高60%標價銷售,銷售一段時間后,甲款型全部售完,乙款型剩余一半,商店決定對乙款型剩余的按標價的五折降價銷售,很快全部售完。求售完這批襯衫商店共獲利多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】動點A從原點出發向數軸負方向運動,同時,動點B也從原點出發向數軸正方向運動,運動到3秒鐘時,兩點相距15個單位長度.已知動點A、B的運動速度比之是3:2(速度單位:1個單位長度/秒).
(1)求兩個動點運動的速度;
(2)A、B兩點運動到3秒時停止運動,請在數軸上標出此時A、B兩點的位置;
(3)若A、B兩點分別從(2)中標出的位置再次同時開始在數軸上運動,運動的速度不變,運動的方向不限,問:經過幾秒鐘,A、B兩點之間相距4個單位長度?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知直角三角形ABC中,∠ACB=90°,E為AB上一點,且CE=EB,ED⊥CB于D,則下列結論中不一定成立的是( )

A.AE=BEB.CE=![]() ABC.∠CEB=2∠AD.AC=
ABC.∠CEB=2∠AD.AC=![]() AB
AB
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com