|
|
|
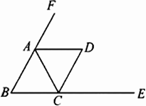
如圖,在△ABC中,AB=AC,∠B=60°,∠FAC、∠ECA是△ABC的兩個外角,AD平分∠FAC,CD平分∠ECA.求證:四邊形ABCD是菱形.
|
|
|
答案:
解析:
|
證明:∵∠B=60°,AB=AC,
∴△ABC為等邊三角形,
∴AB=BC,
∴∠BAC=∠ACB=60°,
∠FAC=∠ACE=120°,
∵AD、CD分別是∠FAC、∠ECA的平分線,
∴ , ,
∴∠BAD=∠BCD=120°,
∴∠D=∠B=60°,
∴四邊形ABCD是平行四邊形.
又∵AB=BC,
∴平行四邊形ABCD是菱形.
|
練習冊系列答案
相關習題
科目:初中數學
來源:新人教版(2012) 八年級下
題型:
|
|
|
如圖,在平行四邊形ABCD中,∠B=110°,延長AD至點F,延長CD至點E,連接EF,則∠E+∠F=
|
| [ ] |
A. |
110°
|
B. |
30°
|
C. |
50°
|
D. |
70°
|
|
|
查看答案和解析>>
科目:初中數學
來源:新人教版(2012) 八年級下
題型:
|
|
|
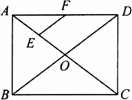
如圖,在矩形ABCD中,對角線AC、BD相交于點O,點E、F分別是AO、AD的中點,若AB=6 cm,BC=8 cm,則△AEF的周長=________cm.
|
|
|
查看答案和解析>>
科目:初中數學
來源:新人教版(2012) 八年級下
題型:
|
|
|
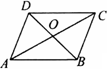
如圖,四邊形ABCD中,對角線AC、BD相交于點O,下列條件中不能判定這個四邊形是平行四邊形的是
|
| [ ] |
A. |
AB∥DC,AD∥BC
|
B. |
AB=DC,AD=BC
|
C. |
AO=CO,BO=DO
|
D. |
AB∥DC,AD=BC
|
|
|
查看答案和解析>>
科目:初中數學
來源:新人教版(2012) 八年級下
題型:
|
|
|
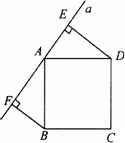
如圖所示,直線a經過正方形ABCD的頂點A,分別過正方形的頂點B、D作BF⊥a于點F,DE⊥a于點E,若DE=8,BF=5,則EF的長為________.
|
|
|
查看答案和解析>>
科目:初中數學
來源:新人教版(2012) 八年級下
題型:
|
|
|
若a<0,則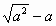 的值是 的值是
|
| [ ] |
A. |
0
|
B. |
-a
|
C. |
-2a
|
D. |
-3a
|
|
|
查看答案和解析>>
科目:初中數學
來源:新人教版(2012) 八年級下
題型:
|
|
|
當1<x<3時,化簡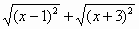 的結果是 的結果是
|
| [ ] |
A. |
4
|
B. |
2x+2
|
C. |
-2x-2
|
D. |
-4
|
|
|
查看答案和解析>>
科目:初中數學
來源:新人教版(2012) 八年級下
題型:
|
|
|
下列二次根式中,能與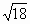 合并的是 合并的是
|
| [ ] |
A. |
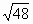
|
B. |
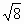
|
C. |
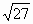
|
D. |
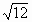
|
|
|
查看答案和解析>>
科目:初中數學
來源:新人教版(2012) 八年級下
題型:
|
|
|
某風景區集體門票的收費標準是20人以內(包括20人),每人25元;超過20人的,超出的人數,每人10元.
(1)寫出應收門票錢數y(元)與游覽人數x(人)(x≥20)之間的函數關系式;
(2)利用(1)中的函數關系式計算:某班54名學生去該風景區游覽時,購買門票花了多少元錢?
|
|
|
查看答案和解析>>

 一諾書業暑假作業快樂假期云南美術出版社系列答案
一諾書業暑假作業快樂假期云南美術出版社系列答案