
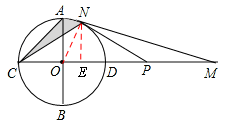
如圖,⊙O的半徑為1,直線CD經過圓心O,交⊙O于C、D兩點,直徑AB⊥CD,點M是直線CD上異于點C、O、D的一個動點,AM所在的直線交于⊙O于點N,點P是直線CD上另一點,且PM=PN.
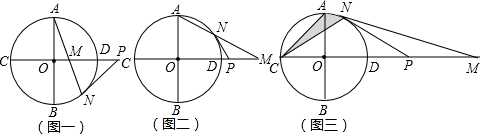
(1)當點M在⊙O內部,如圖一,試判斷PN與⊙O的關系,并寫出證明過程;
(2)當點M在⊙O外部,如圖二,其它條件不變時,(1)的結論是否還成立?請說明理由;
(3)當點M在⊙O外部,如圖三,∠AMO=15°,求圖中陰影部分的面積.
(1)PN與⊙O相切。
(2)成立。
(3)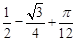 。
。
【解析】
分析:(1)根據切線的判定得出∠PNO=∠PNM+∠ONA=∠AMO+∠ONA進而求出即可。
(2)根據已知得出∠PNM+∠ONA=90°,進而得出∠PNO=180°﹣90°=90°即可得出答案。
(3)首先根據外角的性質得出∠AON=30°,進而由 ,利用扇形面積和三角形面積公式得出即可。
,利用扇形面積和三角形面積公式得出即可。
解:(1)PN與⊙O相切。證明如下:
連接ON,則∠ONA=∠OAN,
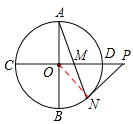
∵PM=PN,∴∠PNM=∠PMN。
∵∠AMO=∠PMN,∴∠PNM=∠AMO。
∴∠PNO=∠PNM+∠ONA=∠AMO+∠ONA=90°。
∵ON是⊙O的半徑,∴PN與⊙O相切。
(2)成立。理由如下:
連接ON,則∠ONA=∠OAN。
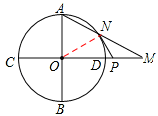
∵PM=PN,∴∠PNM=∠PMN。
在Rt△AOM中,∵∠OMA+∠OAM=90°,
∴∠PNM+∠ONA=90°。∴∠PNO=180°﹣90°=90°。
∵ON是⊙O的半徑,∴PN與⊙O相切。
(3)連接ON,由(2)可知∠ONP=90°,
∵∠AMO=15°,PM=PN,
∴∠PNM=15°,∠OPN=30°。
∴∠PON=60°,∠AON=30°。
作NE⊥OD,垂足為點E,
則NE=ON•sin60°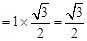 。
。
∴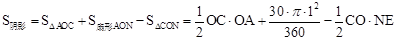
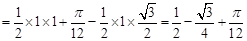 。
。


科目:初中數學 來源: 題型:
 如圖,⊙O的半徑為
如圖,⊙O的半徑為| 5 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com