
如圖,在平面直角坐標系 中,已知點
中,已知點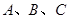 在雙曲線
在雙曲線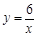 上,
上, 軸于D,
軸于D, 軸于
軸于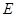 ,點
,點 在
在 軸上,且
軸上,且 ,則圖中陰影部分的面積之和為
,則圖中陰影部分的面積之和為
| A.6 | B.12 | C.18 | D.24 |
B
解析試題分析:過A作AG垂直于x軸,交x軸于點G,由AO=AF,利用三線合一得到G為OF的中點,根據等底同高得到三角形AOD的面積等于三角形AFD的面積,再由A,B及C三點都在反比例函數圖象上,根據反比例的性質得到三角形BOD,三角形COE及三角形AOG的面積都相等,都為 ,由反比例解析式中的k值代入,求出三個三角形的面積,根據陰影部分的面積等于三角形BOD的面積+三角形COE的面積+三角形AOG的面積+三角形AFG的面積=4三角形AOD的面積,即為2|k|,即可得到陰影部分的面積之和.
,由反比例解析式中的k值代入,求出三個三角形的面積,根據陰影部分的面積等于三角形BOD的面積+三角形COE的面積+三角形AOG的面積+三角形AFG的面積=4三角形AOD的面積,即為2|k|,即可得到陰影部分的面積之和.
解:過A作AG⊥x軸,交x軸于點G
∵AO=AF,AG⊥OF,
∴G為OF的中點,即OG=FG,
∴S△OAG=S△FAG,
又A,B及C點都在反比例函數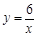 上,
上,
∴S△OAG=S△BOD=S△COE= =3,
=3,
∴S△OAG=S△BOD=S△COE=S△FAG=3,
則S陰影=S△OAG+S△BOD+S△COE+S△FAG=12,
故選B.
考點:反比例函數的性質,等腰三角形的性質,三角形的面積公式
點評:反比例函數 (k≠0)圖象上的點到坐標軸的垂線,此點到原點的連線及坐標軸圍成的直角三角形的面積等于
(k≠0)圖象上的點到坐標軸的垂線,此點到原點的連線及坐標軸圍成的直角三角形的面積等于 ,熟練掌握此性質是解本題的關鍵.
,熟練掌握此性質是解本題的關鍵.


科目:初中數學 來源: 題型:單選題
如圖,Rt△ABC的頂點A在雙曲線 的圖象上,直角邊BC在x軸上,∠ABC=90°,∠ACB=30°,OC=4,連接OA,∠AOB=60°,則k的值是
的圖象上,直角邊BC在x軸上,∠ABC=90°,∠ACB=30°,OC=4,連接OA,∠AOB=60°,則k的值是
A. | B. | C. | D. |
查看答案和解析>>
科目:初中數學 來源: 題型:單選題
如圖,直線y=mx與雙曲線 交于A,B兩點,過點A作AM⊥x軸,垂足為點M,連接BM,若S△ABM=2,則k的值為
交于A,B兩點,過點A作AM⊥x軸,垂足為點M,連接BM,若S△ABM=2,則k的值為
| A.﹣2 | B.2 | C.4 | D.﹣4 |
查看答案和解析>>
科目:初中數學 來源: 題型:單選題
某廠現有300噸煤,這些煤能燒的天數y與平均每天燒的噸數x之間的函數關系是( )
A.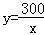 (x>0) (x>0) | B.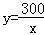 (x≥0) (x≥0) |
| C.y=300x(x≥0) | D.y=300x(x>0) |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
如圖,點A是反比例函數y=的圖象上﹣點,過點A作AB⊥x軸,垂足為點B,線段AB交反比例函數y=的圖象于點C,則△OAC的面積為 _________ .
查看答案和解析>>
科目:初中數學 來源: 題型:單選題
如圖,函數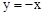 與函數
與函數 的圖象相交于A,B兩點,過A,B兩點分別作y軸的垂線,垂足分別為點C,D.則四邊形ACBD的面積為
的圖象相交于A,B兩點,過A,B兩點分別作y軸的垂線,垂足分別為點C,D.則四邊形ACBD的面積為
A.2 B.4 C.6 D.8
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com