
【題目】如圖,△ABC中,AB=AC=10,BC=12,點D在邊BC上,且BD=4,以點D為頂點作∠EDF=∠B,分別交邊AB于點E,交AC或延長線于點F. 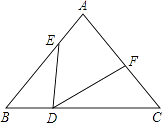
(1)當AE=4時,求AF的長;
(2)當以邊AC為直徑的⊙O與線段DE相切時,求BE的長.
【答案】
(1)解:∵∠EDF+∠FDC=∠B+∠DEB,∠EDF=∠B,
∴∠FDC=∠DEB,
∵AB=AC,
∴∠C=∠B,
∴△CDF∽△BED,
∴ ![]() ,即
,即 ![]() ,
,
解得:CF= ![]() ,
,
∴AF=AC﹣CF=10﹣ ![]()
(2)解:取邊AC中點O,作OG⊥DE于G,OQ⊥BC于Q,過點A作AH⊥BC于H,連接OD,如圖所示:
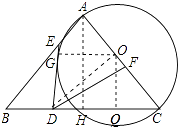
∵AB=AC,AH⊥BC,
∴CH= ![]() BC=6,
BC=6,
∵⊙O和線段DE相切,
∴OG= ![]() AC=5,
AC=5,
在Rt△CAH中,∠AHC=90°,cosC= ![]() ,
,
在Rt△CQO中,∠CQO=90°
∵cosC= ![]() ,
,
∴CQ=COcosC=5× ![]() =3,
=3,
∴DQ=BC﹣BD﹣CQ=12﹣4﹣3=5,
∴OG=DQ,
在Rt△OGD與Rt△DQO中, ![]() ,
,
∴Rt△OGD≌Rt△DQO(HL),
∴∠GOD=∠QDO,
∴OG∥BC,
∴∠EDB=∠OGD=90°,
∴cosB= ![]() =cosC=
=cosC= ![]() ,
,
∴BE= ![]() ,
,
∴當以邊AC為直徑的⊙O與線段DE相切時,BE= ![]() .
.
【解析】(1)先證△BDE∽△CFD,得出對應邊成比例,求出CF的長,即可得出結果;(2)取邊AC中點O,作OG⊥DE于G,OQ⊥BC于Q,過點A作AH⊥BC于H,連接OD,則CH= ![]() BC=6,由⊙O和線段DE相切,得出OG=
BC=6,由⊙O和線段DE相切,得出OG= ![]() AC=5,求出cosC=
AC=5,求出cosC= ![]() =
= ![]() ,CQ=COcosC=3,DQ=BC﹣BD﹣CQ=5,得出OG=DQ,由HL證得Rt△OGD≌Rt△DQO,得出∠GOD=∠QDO,OG∥BC,∠EDB=∠OGD=90°,由cosB=
,CQ=COcosC=3,DQ=BC﹣BD﹣CQ=5,得出OG=DQ,由HL證得Rt△OGD≌Rt△DQO,得出∠GOD=∠QDO,OG∥BC,∠EDB=∠OGD=90°,由cosB= ![]() =cosC=
=cosC= ![]() ,即可得出結果.
,即可得出結果.
【考點精析】根據題目的已知條件,利用等腰三角形的性質和切線的性質定理的相關知識可以得到問題的答案,需要掌握等腰三角形的兩個底角相等(簡稱:等邊對等角);切線的性質:1、經過切點垂直于這條半徑的直線是圓的切線2、經過切點垂直于切線的直線必經過圓心3、圓的切線垂直于經過切點的半徑.


 導學全程練創優訓練系列答案
導學全程練創優訓練系列答案科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,∠ABC=90°,D是邊AC上的一點,連接BD,使∠A=2∠1,E是BC上的一點,以BE為直徑的⊙O經過點D. 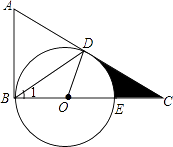
(1)求證:AC是⊙O的切線;
(2)若∠A=60°,⊙O的半徑為2,求陰影部分的面積.(結果保留根號和π)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知y=﹣x+m(m>4)過動點A(m,0),并與反比例函數y= ![]() 的圖象交于B、C兩點(點B在點C的左邊),以OA為直徑作反比例函數y=
的圖象交于B、C兩點(點B在點C的左邊),以OA為直徑作反比例函數y= ![]() 的圖象相交的半圓,圓心為P,過點B作x軸的垂線,垂足為E,并于半圓P交于點D.
的圖象相交的半圓,圓心為P,過點B作x軸的垂線,垂足為E,并于半圓P交于點D. 
(1)當m=5時,求B、C兩點的坐標.
(2)求證:無論m取何值,線段DE的長始終為定值.
(3)記點C關于直線DE的對稱點為C′,當四邊形CDC′E為菱形時,求m的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,Rt△ABC中AB=3,BC=4,∠B=90°,點B、C在兩坐標軸上滑動.當邊AC⊥x軸時,點A剛好在雙曲線 ![]() 上,此時下列結論不正確的是( )
上,此時下列結論不正確的是( )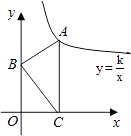
A.點B為(0, ![]() )
)
B.AC邊的高為 ![]()
C.雙曲線為 ![]()
D.此時點A與點O距離最大
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,正方形ABCD中,以對角線BD為邊作菱形BDFE,使B,C,E三點在同一直線上,連接BF,交CD與點G. 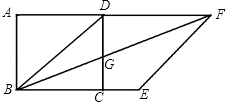
(1)求證:CG=CE;
(2)若正方形邊長為4,求菱形BDFE的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩位同學做拋骰子(均勻正方體形狀)實驗,他們共拋了60次,出現向上點數的次數如表:
向上點數 | 1 | 2 | 3 | 4 | 5 | 6 |
出現次數 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)計算出現向上點數為6的頻率.
(2)丙說:“如果拋600次,那么出現向上點數為6的次數一定是100次.”請判斷丙的說法是否正確并說明理由.
(3)如果甲乙兩同學各拋一枚骰子,求出現向上點數之和為3的倍數的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小軒從如圖所示的二次函數y=ax2+bx+c(a≠0)的圖象中,觀察得出了下面五條信息: ①ab>0;②a+b+c<0;③b+2c>0;④a﹣2b+4c>0;⑤ ![]() .
.
你認為其中正確信息的個數有( )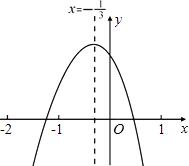
A.2個
B.3個
C.4個
D.5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線經過原點o和x軸上一點A(4,0),拋物線頂點為E,它的對稱軸與x軸交于點D.直線y=﹣2x﹣1經過拋物線上一點B(﹣2,m)且與y軸交于點C,與拋物線的對稱軸交于點F.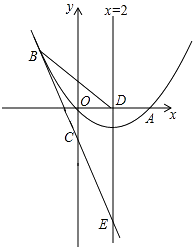
(1)求m的值及該拋物線對應的解析式;
(2)P(x,y)是拋物線上的一點,若S△ADP=S△ADC , 求出所有符合條件的點P的坐標;
(3)點Q是平面內任意一點,點M從點F出發,沿對稱軸向上以每秒1個單位長度的速度勻速運動,設點M的運動時間為t秒,是否能使以Q、A、E、M四點為頂點的四邊形是菱形.若能,請直接寫出點M的運動時間t的值;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某鄉鎮企業生產部有技術工人15人,生產部為了合理制定產品的每月生產定額,統計了這15人某月的加工零件個數:
每人加工零件個數 | 540 | 450 | 300 | 240 | 210 | 120 |
人數 | 1 | 1 | 2 | 6 | 3 | 2 |
(1)寫出這15人該月加工零件數的平均數、中位數和眾數.
(2)假如生產部負責人把每位工人的月加工零件個數定為260,你認為這個定額是否合理?為什么?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com