
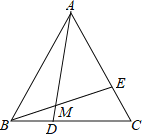
【題目】已知:如圖,△ABC是等邊三角形,點(diǎn)D、E分別在BC,AC且BD=CE,AD、BE相交于點(diǎn)M,

求證:(1)△AME∽△BAE;(2)BD2=AD×DM.
【答案】(1)見解析;(2)見解析.
【解析】
(1)根據(jù)等邊三角形的性質(zhì)可得出AB=BC、∠ABD=∠C,結(jié)合BD=CE即可證出△ABD≌△BCE(SAS),根據(jù)全等三角形的性質(zhì)可得出∠CBE=∠BAD,通過角的計算可得出∠EAM=∠EBA,再結(jié)合∠AEM=∠BEA即可證出△AME∽△BAE;
(2)根據(jù)相似三角形的性質(zhì)可得出∠AME=∠BAE=60°,由對頂角相等可得出∠BMD=60°,再結(jié)合∠ABD=60°、∠BDM=∠ADB,即可證出△ABD∽△BMD,根據(jù)相似三角形的性質(zhì)可證出BD2=AD×DM.
證明:(1)∵△ABC是等邊三角形,
∴AB=BC,∠ABD=∠C=60°.
在△ABD和△BCE中, ,
,
∴△ABD≌△BCE(SAS),
∴∠CBE=∠BAD,
∴∠EAM=∠EBA.
又∵∠AEM=∠BEA,
∴△AME∽△BAE.
(2)∵△AME∽△BAE,
∴∠AME=∠BAE=60°,
∴∠BMD=60°.
又∵∠ABD=60°,∠BDM=∠ADB,
∴△ABD∽△BMD,
∴BD2=AD×DM.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
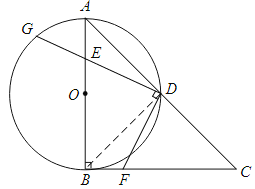
【題目】如圖,在RtΔABC中,∠ABC=90°,AB=CB,以AB為直徑的⊙O交AC于點(diǎn)D,點(diǎn)E是AB邊上一點(diǎn)(點(diǎn)E不與點(diǎn)A、B重合),DE的延長線交⊙O于點(diǎn)G,DF⊥DG,且交BC于點(diǎn)F.
(1)求證:AE=BF;
(2)連接EF,求證:∠FEB=∠GDA;
(3)連接GF,若AE=2,EB=4,求ΔGFD的面積.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】右圖為手的示意圖,在各個手指之間標(biāo)記字母A,B,C,D。請你按圖中箭頭所指的方向(即A→B→C→D→C→B→A→B→C→……的方式)從A開始數(shù)連續(xù)的正整數(shù)1,2,3,4,5,6,7,8,9,……

(1)當(dāng)數(shù)到14時,對應(yīng)的字母是_________;
(2)當(dāng)字母C第201次出現(xiàn)時。恰好數(shù)到的數(shù)是_________;
(3)當(dāng)字母C第2n+1次出現(xiàn)時(n為正整數(shù)),恰好數(shù)到的數(shù)是__________(用含有n的代數(shù)式表示)
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知:∠AOB和兩點(diǎn)C、D,求作一點(diǎn)P,使PC=PD,且點(diǎn)P到∠AOB的兩邊的距離相等.
(要求:用尺規(guī)作圖,保留作圖痕跡,寫出作法,不要求證明).

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖①,梯形ABCD中,AD∥BC,∠C=90°,BA=BC.動點(diǎn)E、F同時從點(diǎn)B出發(fā),點(diǎn)E沿折線 BA–AD–DC運(yùn)動到點(diǎn)C時停止運(yùn)動,點(diǎn)F沿BC運(yùn)動到點(diǎn)C時停止運(yùn)動,它們運(yùn)動時的速度都是1 cm/s.設(shè)E出發(fā)t s時,△EBF的面積為y cm2.已知y與t的函數(shù)圖象如圖②所示,其中曲線OM為拋物線的一部分,MN、NP為線段.
請根據(jù)圖中的信息,解答下列問題:
(1)AD= cm,BC= cm;
(2)求a的值,并用文字說明點(diǎn)N所表示的實(shí)際意義;
(3)直接寫出當(dāng)自變量t為何值時,函數(shù)y的值等于5.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在Rt△ABC中,∠B=90°,∠A=30°,AC=2![]() .
.
(1)利用尺規(guī)作線段AC的垂直平分線DE,垂足為E,交AB于點(diǎn)D;(保留作圖痕跡,不寫作法)
(2)若△ADE的周長為a,先化簡T=(a+1)2﹣a(a﹣1),再求T的值.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知,如圖,A、B分別為數(shù)軸上的兩點(diǎn),A點(diǎn)對應(yīng)的數(shù)為-20,B點(diǎn)對應(yīng)的數(shù)為100.
![]()
請寫出AB中點(diǎn)M對應(yīng)的數(shù)。
(2)現(xiàn)有一只電子螞蟻P從B點(diǎn)出發(fā),以6單位/秒的速度向左運(yùn)動,同時另一只電子螞蟻Q恰好從A點(diǎn)出發(fā),以4單位/秒的速度向右運(yùn)動。設(shè)兩只電子螞蟻在數(shù)軸上的C點(diǎn)相遇,你知道C點(diǎn)對應(yīng)的數(shù)是多少嗎?
(3)若當(dāng)電子螞蟻P從B點(diǎn)出發(fā)時,以6單位/秒的速度向左運(yùn)動,同時另一只電子螞蟻Q恰好從A點(diǎn)出發(fā),以4單位/秒的速度也向左運(yùn)動。設(shè)兩只電子螞蟻在數(shù)軸上的D點(diǎn)相遇,你知道D點(diǎn)對應(yīng)的數(shù)是多少嗎?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,Rt△ABC中,∠C=90°,AC=![]() ,tanB=
,tanB=![]() .半徑為2的⊙C, 分別交AC、BC于點(diǎn)D、E,得到
.半徑為2的⊙C, 分別交AC、BC于點(diǎn)D、E,得到![]() .
.
(1)求證:AB為⊙C的切線;
(2)求圖中陰影部分的面積.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】自學(xué)下面材料后,解答問題.
分母中含有未知數(shù)的不等式叫分式不等式.如:![]() ;
;![]() 等.那么如何求出它們的解集呢?根據(jù)我們學(xué)過的有理數(shù)除法法則可知:兩數(shù)相除,同號得正,異號得負(fù).其字母表達(dá)式為:
等.那么如何求出它們的解集呢?根據(jù)我們學(xué)過的有理數(shù)除法法則可知:兩數(shù)相除,同號得正,異號得負(fù).其字母表達(dá)式為:
(1)若![]() >0,
>0,![]() >0,則
>0,則![]() >0;若
>0;若![]() <0,
<0,![]() <0,則
<0,則![]() >0;
>0;
(2)若![]() >0,
>0,![]() <0,則
<0,則![]() <0;若
<0;若![]() <0,
<0,![]() >0,則
>0,則![]() <0.
<0.
反之:(1)若![]() >0,則
>0,則![]() 或
或![]()
(2)若![]() <0,則__________或__________.
<0,則__________或__________.
(3)根據(jù)上述規(guī)律,求不等式![]() 的解集.
的解集.
(4)試求不等式![]() 的解集.
的解集.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com