
【題目】為引導學生廣泛閱讀文學名著,某校在七年級、八年級開展了讀書知識競賽.該校七、八年級各有學生400人,各隨機抽取20名學生進行了抽樣調查,獲得了他們知識競賽成績(分),并對數據進行整理、描述和分析.下面給出了部分信息.
七年級:
74 97 96 89 98 74 65 76 72 78 99 72 97 76 99 74 99 73 98 74
八年級:
76 88 93 65 78 94 89 68 95 50 89 88 89 89 77 94 87 88 92 91
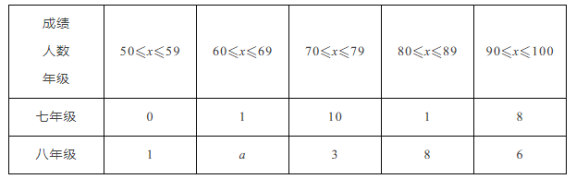
平均數、中位數、眾數如表所示:
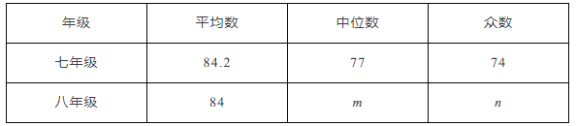
根據以上信息,回答下列問題:
(1)![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)該校對讀書知識競賽成績不少于80分的學生授予“閱讀小能手”稱號,請你估計該校七、八年級所有學生中獲得“閱讀小能手”稱號的大約有______人;
(3)結合以上數據,你認為哪個年級讀書知識競賽的總體成績較好,說明理由.
【答案】(1)2,88.5,89;(2)460;(3)八年級讀書知識競賽的總體成績較好,見解析.
【解析】
(1)根據總數據可得a的值,根據中位數和眾數的定義可得m和n的值;
(2)分別計算該校七、八年級所有學生中獲得“閱讀小能手”稱號的人數,相加可得結論;
(3)根據平均數,眾數和中位數這幾方面的意義解答可得.
解:(1)a=20-1-3-8-6=2,
八年級20人的成績排序后為:50,65,68,76,77,78,87,88,88,88,89,89,89,89,91,92,93,94,94,95,因為有20人,所以中位數為成績排名第10和第11位的分數的平均數,觀察成績數據89分的人數最多,
∴m=![]() =88.5,n=89,
=88.5,n=89,
故答案為:2,88.5,89;
(2)![]() ,
,
則估計該校七、八年級所有學生中獲得“閱讀小能手”稱號的大約有460人.
故答案為:460;
(3)∵八年級讀書知識競賽的總體成績的眾數高于七年級,且八年級的中位數89高于七年級的中位數74,說明八年級分數不低于89分的人數比七年級多,
∴八年級讀書知識競賽的總體成績較好.


 高中必刷題系列答案
高中必刷題系列答案科目:初中數學 來源: 題型:
【題目】如圖:在數軸上點![]() 表示數
表示數![]() ,點
,點![]() 表示數
表示數![]() ,點
,點![]() 表示數
表示數![]() ,
,![]() 是多項式
是多項式![]() 的一次項系數,
的一次項系數,![]() 是絕對值最小的整數,單項式
是絕對值最小的整數,單項式![]() 的次數為
的次數為![]() .
.
![]()
(1)![]() = ,
= ,![]() = ,
= ,![]() = ;
= ;
(2)若將數軸在點![]() 處折疊,則點
處折疊,則點![]() 與點
與點![]() 重合( 填“能”或“不能”);
重合( 填“能”或“不能”);
(3)點![]() 開始在數軸上運動,若點
開始在數軸上運動,若點![]() 以每秒1個單位長度的速度向右運動,同時,點
以每秒1個單位長度的速度向右運動,同時,點![]() 和點
和點![]() 分別以每秒3個單位長度和2個單位長度的速度向左運動,
分別以每秒3個單位長度和2個單位長度的速度向左運動,![]() 秒鐘過后,若點
秒鐘過后,若點![]() 與點B之間的距離表示為
與點B之間的距離表示為![]() ,點
,點![]() 與點
與點![]() 之間的距離表示為
之間的距離表示為![]() ,則
,則![]() = ,
= , ![]() = (用含
= (用含![]() 的代數式表示);
的代數式表示);
(4)請問:AB+BC的值是否隨著時間![]() 的變化而改變?若變化,請說明理由;若不變,請求其值.
的變化而改變?若變化,請說明理由;若不變,請求其值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商店銷售10臺A型和20臺B型電腦的利潤為4000元,銷售20臺A型和10臺B型電腦的利潤為3500元.
(1)求每臺A型電腦和B型電腦的銷售利潤;
(2)該商店計劃一次購進兩種型號的電腦共100臺,其中B型電腦的進貨量不超過A型電腦的2倍,設購進A型電腦x臺,這100臺電腦的銷售總利潤為y元.
①求y關于x的函數關系式;
②該商店購進A型、B型電腦各多少臺,才能使銷售總利潤最大?
(3)實際進貨時,廠家對A型電腦出廠價下調m(0<m<100)元,且限定商店最多購進A型電腦70臺.若商店保持兩種電腦的售價不變,請你根據以上信息及(2)中條件,設計出使這100臺電腦銷售總利潤最大的進貨方案.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】直線![]() 與直線
與直線![]() 垂直相交于點
垂直相交于點![]() ,點
,點![]() 在射線
在射線![]() 上運動(點
上運動(點![]() 不與點
不與點![]() 重合),點
重合),點![]() 在射線
在射線![]() 上運動(點
上運動(點![]() 不與點
不與點![]() 重合).
重合).
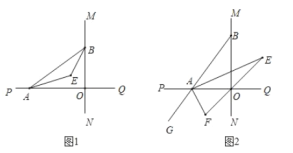
(1)如圖1,已知![]() 、
、![]() 分別是
分別是![]() 和
和![]() 的角平分線,
的角平分線,
①當![]() 時,求
時,求![]() 的度數;
的度數;
②點![]() 在運動的過程中,
在運動的過程中,![]() 的大小是否會發生變化?若發生變化,請說明變化的情況;若不發生變化,試求出
的大小是否會發生變化?若發生變化,請說明變化的情況;若不發生變化,試求出![]() 的大小;
的大小;
(2)如圖2,延長![]() 至
至![]() ,已知
,已知![]() 、
、![]() 的角平分線與
的角平分線與![]() 的角平分線所在的直線分別相交于
的角平分線所在的直線分別相交于![]() 、
、![]() ,在
,在![]() 中,如果有一個角是另一個角的3倍,請直接寫出
中,如果有一個角是另一個角的3倍,請直接寫出![]() 的度數.
的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
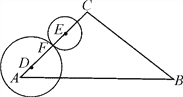
【題目】如圖,在△ABC中,∠A=45°,AB=![]() ,AC=6,點D,E為邊AC上的點,AD=1,CE=2,點F為線段DE上一點(不與D,E重合),分別以點D、E為圓心,DF、EF為半徑作圓.若兩圓與邊AB,BC共有三個交點時,線段DF長度的取值范圍是_______.
,AC=6,點D,E為邊AC上的點,AD=1,CE=2,點F為線段DE上一點(不與D,E重合),分別以點D、E為圓心,DF、EF為半徑作圓.若兩圓與邊AB,BC共有三個交點時,線段DF長度的取值范圍是_______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀材料:若a,b都是非負實數,則a+b≥2![]() .當且僅當a=b時,“=”成立.
.當且僅當a=b時,“=”成立.
證明:∵(![]() )2≥0,∴a-2
)2≥0,∴a-2![]() +b≥0.
+b≥0.
∴a+b≥2![]() .當且僅當a=b時,“=”成立.
.當且僅當a=b時,“=”成立.
舉例應用:已知x>0,求函數y=x![]() 的最小值.
的最小值.
解:y=x![]() =2
=2![]() .當且僅當x=
.當且僅當x=![]() ,即x=
,即x=![]() 時,“=”成立.
時,“=”成立.
∴當x=![]() 時,函數取得最小值,y最小=2
時,函數取得最小值,y最小=2![]() .
.
問題解決:
(1)已知x>0,求函數y=![]() 的最小值;
的最小值;
(2)求代數式![]() (m>-1)的最小值.
(m>-1)的最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】正方形ABCD中,E是BC上一點,F是CD延長線上一點,![]() ,連接AE,AF,EF,G為EF中點,連接AG,DG.
,連接AE,AF,EF,G為EF中點,連接AG,DG.

(1)如圖1:若![]() ,
,![]() ,求DG;
,求DG;
(2)如圖2:延長GD至M,使![]() ,過M作MN∥FD交AF的延長線于N,連接NG,若
,過M作MN∥FD交AF的延長線于N,連接NG,若![]() .求證:
.求證:![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點E,F分別是銳角∠A兩邊上的點,AE=AF,分別以點E,F為圓心,以AE的長為半徑畫弧,兩弧相交于點D,連接DE,DF.
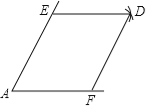
(1)請你判斷所畫四邊形的性狀,并說明理由;
(2)連接EF,若AE=8厘米,∠A=60°,求線段EF的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com