
如圖正方形ABCD和正方形EFGH,F和B重合,EF在AB上,連DH(本題14分)
⑴、由圖⑴易知,
①線段AE=CG, AE和CG所在直線互相垂直,且此時易求得② 。
。
⑵、若把正方形EFGH繞F點逆時針旋轉 度(圖2),⑴中的兩個結論是否仍然成立?若成立,選擇其中一個加以證明,若不成立,請說明理由。
度(圖2),⑴中的兩個結論是否仍然成立?若成立,選擇其中一個加以證明,若不成立,請說明理由。
⑶、若把圖⑴中的正方形EFGH沿BD方向以每秒1cm的速度平移,設平移時間為x秒,正方形ABCD和正方形EFGH的邊長分別為5cm和1cm,
①在平移過程中,△AFH是否會成為等腰三角形?若能求出x的值,若不能,說明理由.
②在平移過程中,△AFH是否會成為等邊三角形?若能求出x的值,若不能,設正方形ABCD和正方形EFGH的邊長分別為acm和bcm,則當a、b滿足什么關系時,△AFH可以成為等邊三角形.

解:(1)∵AE=CG,∴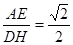
(2)∵正方形ABCD和正方形EFGH,
∴∠ABC=∠=EBG=90°,
∴∠α=90°-∠ABG,∠CBG=90°-∠ABG,
∴∠α=∠CBG,
由于AB=BC,EB=BG,
∴△AEB≌△CGB,∴AE=CG.
∴(1)中的兩個結論都成立.
1,當ABCD邊長=5,EFGH=1時候,,△AFH不會成為等邊三角形。
設ABCD邊長為a,EFGH邊長為b,連接AC,AC與BD相交于K點(AC與BD相互垂直平分,不用證明了吧)
AK =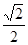 a,FK=
a,FK=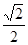 b,
b,
AF2=AK2 +FK2,既AF2=a2 /2+b2/2
若△AFH為等邊三角形,那么AK=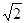 b
b
所以:2b2=a2/2+b2/2
即:a:b=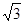 :1
:1
所以:當ABCD的邊長是EFGH邊長的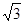 倍時候,△AFH可以為正三角形。
倍時候,△AFH可以為正三角形。
【解析】(1)連接DB,可證明△DHG≌△DHE,再由AE=CG,可直接得出結論.
(2)先求證∠α和∠CBG相等,利用SAS求證△AEB≌△CBG,即可.
(3)①根據等腰三角形的性質,考慮底和腰的特征即可;
②根據等邊三角形的性質即可得到結果。


科目:初中數學 來源: 題型:
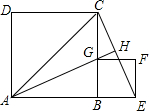 (2011•利川市一模)如圖,ABCD和BEFG都是正方形,A、B、E三點在同一直線上,連接AC、EC、AG,延長AG交EC于H.
(2011•利川市一模)如圖,ABCD和BEFG都是正方形,A、B、E三點在同一直線上,連接AC、EC、AG,延長AG交EC于H.查看答案和解析>>
科目:初中數學 來源:2012-2013學年江蘇灌南實驗中學九年級第一次階段性檢測數學試卷(帶解析) 題型:解答題
如圖正方形ABCD和正方形EFGH,F和B重合,EF在AB上,連DH(本題14分)
⑴、由圖⑴易知,
①線段AE=CG, AE和CG所在直線互相垂直,且此時易求得② 。
。
⑵、若把正方形EFGH繞F點逆時針旋轉 度(圖2),⑴中的兩個結論是否仍然成立?若成立,選擇其中一個加以證明,若不成立,請說明理由。
度(圖2),⑴中的兩個結論是否仍然成立?若成立,選擇其中一個加以證明,若不成立,請說明理由。
⑶、若把圖⑴中的正方形EFGH沿BD方向以每秒1cm的速度平移,設平移時間為x秒,正方形ABCD和正方形EFGH的邊長分別為5cm和1cm,
①在平移過程中,△AFH是否會成為等腰三角形?若能求出x的值,若不能,說明理由.
②在平移過程中,△AFH是否會成為等邊三角形?若能求出x的值,若不能,設正方形ABCD和正方形EFGH的邊長分別為acm和bcm,則當a、b滿足什么關系時,△AFH可以成為等邊三角形.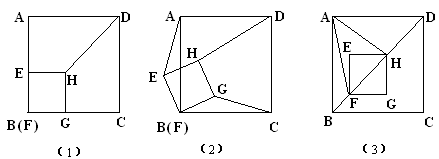
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com