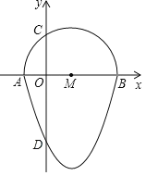
【題目】如圖，我們把一個半圓與拋物線的一部分圍成的封閉圖形稱為“果圓”，已知點
、
、
、
分別是“果圓”與坐標軸的交點，拋物線的解析式為
，
為半圓的直徑，則這個“果圓”被
軸截得的弦
的長為_________．
科目：初中數學 來源： 題型：
【題目】某校學生會干部對全校師生倡導的“武漢加油”的自愿捐款活動進行抽樣調查，得到一組學生捐款情況的數據，對學校部分捐款人數進行調查和分組統計后，將數據整理成如圖所示的統計圖（圖中信息不完整）．已知A、B兩組捐款人數的比為1∶5．
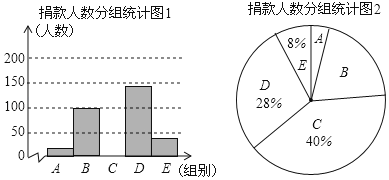
組別 | 捐款額x（元） | 人數 |
A | 1≤x＜10 | a |
B | 10≤x＜20 | 100 |
C | 20≤x＜30 | |
D | 30≤x＜40 | |
E | 40≤x＜50 |
請結合以上信息解答下列問題．
（1）a＝ ，本次調查樣本的容量是 ；
（2）先求出C組的人數，再補全“捐款人數分組統計圖1”；
（3）根據統計情況，估計該校參加捐款的5000名學生有多少人捐款在20至50元之間．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】為了解某地區企業信息化發展水平，從該地區中隨機抽取50家企業調研，針對體現企業信息化發展水平的A和B兩項指標進行評估，獲得了它們的成績（十分制），并對數據（成績）進行整理、描述和分析．下面給出了部分信息．
a．A項指標成績的頻數分布直方圖如下（數據分成6組：
，
，
，
，
，
）：
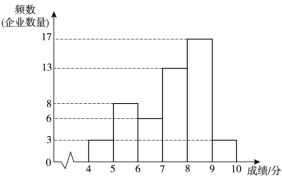
b．A項指標成績在這一組的是：
7.2 7.3 7.5 7.67 7.7 7.71 7.75 7.82 7.86 7.9 7.92 7.93 7.97
c．
兩項指標成績的平均數、中位數、眾數如下：
平均數 | 中位數 | 眾數 | |
A項指標成績 | 7.37 | m | 8.2 |
B項指標成績 | 7.21 | 7.3 | 8 |
根據以上信息，回答下列問題：
（1）寫出表中m的值
（2）在此次調研評估中，某企業A項指標成績和B項指標成績都是7.5分，該企業成績排名更靠前的指標是______________（填“A”或“B”），理由是_____________；
（3）如果該地區有500家企業，估計A項指標成績超過7.68分的企業數量．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，把某矩形紙片ABCD沿EF、GH折疊（點E、H在AD邊上，點F、G在BC邊上），使得點B、點C落在AD邊上同一點P處，A點的對稱點為
點，D點的對稱點為
點，若
，
的面積為4，
的面積為1，則矩形ABCD的面積等于_____.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商場服裝部為了調動營業員的積極性，決定實行目標管理，根據目標完成的情況對營業員進行適當的獎勵．為了確定一個適當的月銷售目標，商場服裝部統計了每位營業員在某月的銷售額(單位：萬元)，數據如下：
17 | 18 | 16 | 13 | 24 | 15 | 28 | 26 | 18 | 19 |
22 | 17 | 16 | 19 | 32 | 30 | 16 | 14 | 15 | 26 |
15 | 32 | 23 | 17 | 15 | 15 | 28 | 28 | 16 | 19 |
對這30個數據按組距3進行分組，并整理、描述和分析如下：
頻數分布表
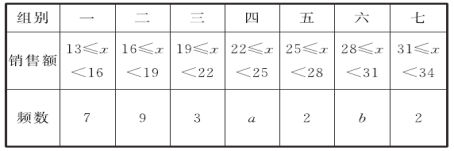
數據分析表
平均數 | 眾數 | 中位數 |
20.3 | c | 18 |
請根據以上信息解答下列問題：
(1)填空：a＝____，b＝_____，c＝_____；
(2)若將月銷售額不低于25萬元確定為銷售目標，則有______位營業員獲得獎勵；
(3)若想讓一半左右的營業員都能達到銷售目標，你認為月銷售額定為多少合適？說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
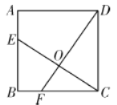
【題目】如圖，已知正方形
的邊長為
，點
，
分別在邊
，
上，且
，
，
相交于點
，下列結論：①
；②
；③
；④
的面積等于四邊形
的面積，其中正確的有（ ）
A.
個B.
個C.
個D.個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】對垃圾進行分類投放，能提高垃圾處理和再利用的效率，減少污染，保護環境．為了檢查垃圾分類的落實情況，某居委會成立了甲、乙兩個檢查組，采取隨機抽查的方式分別對轄區內的A，B，C，D四個小區進行檢查，并且每個小區不重復檢查．
（1）甲組抽到A小區的概率是多少；
（2）請用列表或畫樹狀圖的方法求甲組抽到A小區，同時乙組抽到C小區的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，可以自由轉動的轉盤被它的兩條直徑分成了四個分別標有數字的扇形區域，其中標有數字“1”的扇形的圓心角為120°．轉動轉盤，待轉盤自動停止后，指針指向一個扇形的內部，則該扇形內的數字即為轉出的數字，此時，稱為轉動轉盤一次(若指針指向兩個扇形的交線，則不計轉動的次數，重新轉動轉盤，直到指針指向一個扇形的內部為止)．
（1）轉動轉盤一次，求轉出的數字是﹣2的概率；
（2）轉動轉盤兩次，用樹狀圖或列表法求這兩次分別轉出的數字之積為正數的概率．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】思維啟迪：
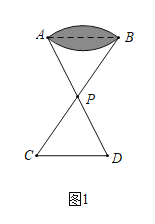
（1）如圖1，
，
兩點分別位于一個池塘的兩端，小亮想用繩子測量，間的距離，但繩子不夠長，聰明的小亮想出一個辦法：先在地上取一個可以直接到達點的點
，連接
，取的中點
（點可以直接到達點），利用工具過點作
交
的延長線于點
，此時測得
，那么，間的距離是______
．
思維探索：
（2）在
和
中，
，
，且
，
．將繞點順時針旋轉，把點
在
邊上時的位置作為起始位置（此時點和點位于的兩側），設旋轉角為
，連接
，點是線段的中點，連接
，
．
①如圖2，當在起始位置時，猜想：與的數量關系和位置關系分別是_______；_______．
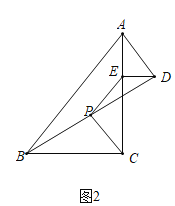
②如圖3，當
，點落在
邊上，請判斷與的數量關系和位置關系，并證明你的結論．
③當
時，若
，
，請直接寫出
的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
