
【題目】如圖已知二次函數y=ax2圖象的頂點為原點,直線y=![]() x+4的圖象與該二次函數的圖象交于A點(8,8),直線與x軸的交點為C,與y軸的交點為B.
x+4的圖象與該二次函數的圖象交于A點(8,8),直線與x軸的交點為C,與y軸的交點為B.
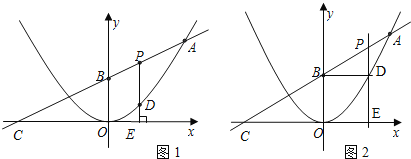
(1)求這個二次函數的解析式與B點坐標;
(2)P為線段AB上的一個動點(點P與A,B不重合),過P作x軸的垂線與這個二次函數的圖象交于D點,與x軸交于點E.設線段PD的長為h,點P的橫坐標為t,求h與t之間的函數關系式,并寫出自變量t的取值范圍(圖1);
(3)在(2)的條件下,連接BD,當動點P在線段AB上移動時,點D也在拋物線上移動,線段BD也繞點B轉動,當BD∥x軸時(圖2),請求出P點的坐標.
【答案】(1)這個二次函數的解析式y=![]() x2.B點的坐標為(0,4).(2)h=﹣
x2.B點的坐標為(0,4).(2)h=﹣![]() t2+
t2+![]() t+4(0<t<8).(3)P點坐標為(4
t+4(0<t<8).(3)P點坐標為(4![]() ,4+2
,4+2![]() ).
).
【解析】
試題分析:(1)由二次函數的圖象過點A(8,8),將其代入函數解析式中即可求得a值,將x=0代入直線方程,即可求得B點坐標;
(2)由P、D橫坐標都為t,將其分別代入二次函數和直線解析式,用t表現出P、D點縱坐標,二者相減即可找到h與t的關系,因為P在線段BA上,由此可找出t的范圍;
(3)BD平行x軸,可知,B、D兩點縱坐標相等,從而求出t值,代入(2)中的P點坐標即可得出結論.
解:(1)∵二次函數y=ax2圖象過點A(8,8),
∴有8=82a=64a,解得a=![]() ,
,
∴這個二次函數的解析式y=![]() x2.
x2.
∵點B為直線y=![]() x+4的圖象與y軸的交點,
x+4的圖象與y軸的交點,
∴當x=0時,y=![]() ×0+4=4,
×0+4=4,
∴B點的坐標為(0,4).
(2)∵P點在線段BA上,
∴P點坐標為(t,![]() t+4)(0<t<8),
t+4)(0<t<8),
∵D點在二次函數圖象上,且P、D橫坐標相等,
∴D點坐標為(t,![]() t2),
t2),
PD=h=![]() t+4﹣
t+4﹣![]() t2=﹣
t2=﹣![]() t2+
t2+![]() t+4(0<t<8).
t+4(0<t<8).
(3)∵當BD∥x軸時,B、D兩點縱坐標相等,且B(0,4)
即4=![]() t2,
t2,
解得t=4![]() .
.
∴P點坐標為(4![]() ,4+2
,4+2![]() ).
).


科目:初中數學 來源: 題型:
【題目】2016年11月17日,我國在酒泉衛星發射中心使用長征二號FY11運載火箭成功將神舟十一號載人飛船送入太空,此次神舟十一號順利升空是中國航天的又一次重大勝利.神舟十一號和天宮二號對接時的軌道高度是393千米,比過去高了50千米.393千米可以用科學記數法表示為( )米.
A.3.93×105
B.3.93×106
C.3.93×104
D.0.393×106
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小亮家與姥姥家相距24km,小亮8:00從家出發,騎自行車去姥姥家.媽媽8:30從家出發,乘車沿相同路線去姥姥家.在同一直角坐標系中,小亮和媽媽的行進路程S(km)與北京時間t(時)的函數圖象如圖所示.根據圖象得到小亮結論,其中錯誤的是( )
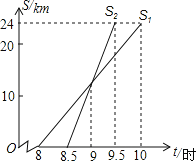
A.小亮騎自行車的平均速度是12km/h
B.媽媽比小亮提前0.5小時到達姥姥家
C.媽媽在距家12km處追上小亮
D.9:30媽媽追上小亮
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在一個口袋里有四個完全相同的小球,把它們分別標號為1,2,3,4,小明和小強采取的摸取方法分別是:
小明:隨機摸取一個小球記下標號,然后放回,再隨機摸取一個小球,記下標號;
小強:隨機摸取一個小球記下標號,不放回,再隨機摸取一個小球,記下標號.
(1)用畫樹狀圖(或列表法)分別表示小明和小強摸球的所有可能出現的結果;
(2)分別求出小明和小強兩次摸球的標號之和等于5的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用白鐵皮做罐頭盒,每張鐵片可制盒身16個或制盒底43個,一個盒身與兩個盒底配成一套罐頭盒,現有150張白鐵皮,用多少張制盒身,多少張制盒底,可以正好制成整套罐頭盒?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知拋物線y=﹣x2+bx+c過點A(1,4),B(﹣2,﹣5)
(1)求此拋物線的解析式;
(2)當y>0時,x的取值范圍是 (直接寫出結果).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】按圖填空, 并注明理由
已知: 如圖, ∠1=∠2, ∠3=∠E. 求證: AD∥BE
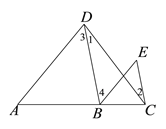
證明: ∵∠1 = ∠2 (已知)
∴ ∥ ( )
∴ ∠E = ∠ ( )
又∵ ∠E = ∠3 ( 已知 )
∴ ∠3 = ∠ ( 等量代換 )
∴ ∥ ( 內錯角相等,兩直線平行 )
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com