
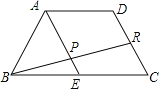
【題目】如圖,AD∥BC,BC=2AD,E為BC的中點,R為DC的中點,BR交AE于點P,則EP:AP= .
【答案】![]() .
.
【解析】
試題分析:先由BC=2AD,BE=EC=![]() BC,得出BE=EC=AD,根據AD∥BC,由一組對邊平行且相等的四邊形是平行四邊形可得四邊形ADCE是平行四邊形,那么EA=CD,EA∥CD.得出△BEP∽△BCR,于是EP=
BC,得出BE=EC=AD,根據AD∥BC,由一組對邊平行且相等的四邊形是平行四邊形可得四邊形ADCE是平行四邊形,那么EA=CD,EA∥CD.得出△BEP∽△BCR,于是EP=![]() CR,而CR=
CR,而CR=![]() CD,那么EP=
CD,那么EP=![]() CD=
CD=![]() EA,然后根據比例的性質即可求出答案即可.
EA,然后根據比例的性質即可求出答案即可.
解:∵BC=2AD,BE=EC=![]() BC,
BC,
∴BE=EC=AD,
∵在等腰梯形ABCD中,AD∥BC,
∴四邊形ADCE是平行四邊形,
∴EA=CD,EA∥CD,
∴△BEP∽△BCR,
∵BE=EC=![]() BC,
BC,
∴EP=![]() CR,
CR,
∵CR=![]() CD,
CD,
∴EP=![]() CD=
CD=![]() EA,
EA,
∴![]() =
=![]() ,
,
∴EP:AP=![]() .
.
故答案為:![]() .
.


科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系xOy中,直線y=![]() x+2與x軸交于點A,與y軸交于點C.拋物線y=ax2+bx+c的對稱軸是x=﹣
x+2與x軸交于點A,與y軸交于點C.拋物線y=ax2+bx+c的對稱軸是x=﹣![]() 且經過A、C兩點,與x軸的另一交點為點B.
且經過A、C兩點,與x軸的另一交點為點B.
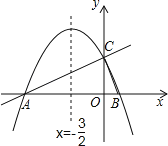
(1)①直接寫出點B的坐標;②求拋物線解析式.
(2)若點P為直線AC上方的拋物線上的一點,連接PA,PC.求△PAC的面積的最大值,并求出此時點P的坐標.
(3)拋物線上是否存在點M,過點M作MN垂直x軸于點N,使得以點A、M、N為頂點的三角形與△ABC相似?若存在,求出點M的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在矩形ABCD中,AB=4cm,AD=12cm,P點在AD邊上以每秒1cm的速度從A向D運動,點Q在BC邊上,以每秒4cm的速度從C點出發,在CB間往返運動,二點同時出發,待P點到達D點為止,在這段時間內,線段PQ有( )次平行于AB.

A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法中,正確的是( )
A. 三角形的內心到三角形的三個頂點的距離相等 B. 三點確定一個圓
C. 垂直于半徑的直線一定是這個圓的切線 D. 任何三角形有且只有一個內切圓
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】有一枚質地均勻的正方體骰子,六個面分別寫有1、2、3、4、5、6的數字,規定“拋擲該枚骰子得到的數字是拋擲后,面朝上的那一個數字”.先后拋擲這枚骰子兩次,得到的數字分別記為b和c,則當x>﹣3時,函數y=x2+bx+c隨x的增大而增大的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com