
【題目】對于一個關于x的代數式A,若存在一個系數為正數關于x的單項式F,使![]() 的結果是所有系數均為整數的整式,則稱單項式F為代數式A的“整系單項式”.例如:
的結果是所有系數均為整數的整式,則稱單項式F為代數式A的“整系單項式”.例如:
當A=![]() ,F=2x3時,由于
,F=2x3時,由于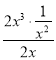 =1,故2x3是
=1,故2x3是![]() 的整系單項式;
的整系單項式;
當A=![]() ,F=6x5時,由于
,F=6x5時,由于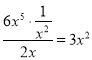 ,故6x5是
,故6x5是![]() 的整系單項式;
的整系單項式;
當A=3-![]() ,F=
,F=![]() 時,由于
時,由于 =2x-1,故
=2x-1,故![]() 是3-
是3-![]() 的整系單項式;
的整系單項式;
當A=3-![]() ,F=8x4時,由于
,F=8x4時,由于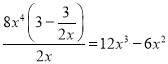 ,故8x4是3-
,故8x4是3-![]() 的整系單項式;
的整系單項式;
顯然,當代數式A存在整系單項式F時,F有無數個,現把次數最低,系數最小的整系單項式F記為F(A).例如:![]() ,
,![]()
閱讀以上材料并解決下列問題:
(1)判斷:當A=![]() 時,F=2x3______A的整系單項式(填“是”或“不是”)
時,F=2x3______A的整系單項式(填“是”或“不是”)
(2)解方程: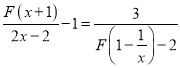
(3)已知a、b、c是△ABC的邊長,其中a、b滿足(a-5)2+![]() =0,且關于x的方程|
=0,且關于x的方程|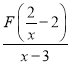 |=c有且只有3個不相等的實數根,求△ABC的周長.
|=c有且只有3個不相等的實數根,求△ABC的周長.
【答案】(1)是;(2)x=![]() ;(3)26或27;
;(3)26或27;
【解析】
(1)當A=![]() 時,F=2x3時,
時,F=2x3時,![]() =x;
=x;
(2)令F=axn,結合定義進行判斷,即可求出F(x+1)=2x,F(1-![]() )=2x2,將所求方程轉化為
)=2x2,將所求方程轉化為![]() -1=
-1=![]() 即可求解;
即可求解;
(3)根據平方與二次根式的性質可求a=5,b=9,再求出F(![]() )=x2,將所求式子轉化為可以化為|
)=x2,將所求式子轉化為可以化為|![]() |=c,結合函數圖象即可求解;
|=c,結合函數圖象即可求解;
解:(1)當A=![]() 時,F=2x3時,
時,F=2x3時,![]() =x,
=x,
∴![]() 是2x3的整系單項式;
是2x3的整系單項式;
(2)F(x+1)=2x,F(1-![]() )=2x2,
)=2x2,
∴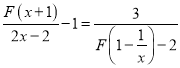 可以化為
可以化為![]() -1=
-1=![]() ,
,
∴2x2-3x+1=0,
∴x=1或x=![]() ;
;
經檢驗x=1是方程的增根,
∴原方程的解為x=![]() ;
;
(3)∵(a-5)2+![]() =0,
=0,
∴a=5,b=9,
F(![]() )=x2,
)=x2,
∴|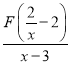 |=c可以化為|
|=c可以化為|![]() |=c,
|=c,
∴|(x-3)+![]() +6|=c,
+6|=c,
當x=6時,c=12,
∴當x≥6時,c≥12,此時方程有且只有3個不相等的實數根,
∵c<14,
∴c=12或c=13,
∴△ABC的周長為26或27;


科目:初中數學 來源: 題型:
【題目】江蘇是全國首個自然村“村村通寬帶”省份.我市某村為了將當地農產品外銷,建立了淘寶網店.該網店于今年7月底以每袋25元的成本價收購一批農產品.當商品售價為每袋40元時,8月份銷售256袋.9、10月該商品十分暢銷.銷售量持續走高.在售價不變的基礎上,10月份的銷售量達到400袋.設9、10這兩個月月平均增長率不變.
(1)求9、10這兩個月的月平均增長率;
(2)為迎接雙“十一”,11月份起,該網店采用降價促銷的方式回饋顧客,經調查發現,該農產品每降價1元/每袋,銷售量就增加5袋,當農產品每袋降價多少元時,該淘寶網店11月份獲利4250元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知矩形![]() 中,
中,![]() ,
,![]() ,點
,點![]() 是邊
是邊![]() 上一點,
上一點,![]() ,連接
,連接![]() .
.
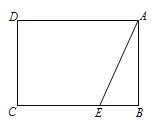
(1)沿![]() 翻折
翻折![]() 使點
使點![]() 落在點
落在點![]() 處,
處,
①連接![]() ,若
,若![]() ,求
,求![]() 的值;
的值;
②連接![]() ,若
,若![]() ,求
,求![]() 的取值范圍.
的取值范圍.
(2)![]() 繞點
繞點![]() 順時針旋轉得
順時針旋轉得![]() ,點
,點![]() 落在邊
落在邊![]() 上時旋轉停止. 若點
上時旋轉停止. 若點![]() 落在矩形對角線
落在矩形對角線![]() 上,且點
上,且點![]() 到
到![]() 的距離小于
的距離小于![]() 時,求
時,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
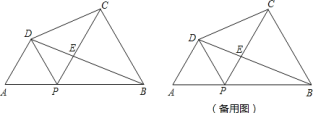
【題目】如圖,已知線段![]() ,
,![]() 是線段
是線段![]() 上任意一點(不與點
上任意一點(不與點![]() 、
、![]() 重合),分別以
重合),分別以![]() 、
、![]() 為邊,在
為邊,在![]() 的同側作等邊
的同側作等邊![]() 和
和![]() ,連接
,連接![]() 與
與![]() 交于點
交于點![]() ,連接
,連接![]() .
.
![]() 當
當![]() 時,試求
時,試求![]() 的正切值;
的正切值;
![]() 若線段
若線段![]() 是線段
是線段![]() 和
和![]() 的比例中項,試求這時
的比例中項,試求這時![]() 的值;
的值;
![]() 記四邊形
記四邊形![]() 的面積為
的面積為![]() ,當
,當![]() 在線段
在線段![]() 上運動時,
上運動時,![]() 與
與![]() 是否成正比例,若成正比例,試求出比例系數;若不成正比例,試說明理由.
是否成正比例,若成正比例,試求出比例系數;若不成正比例,試說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】初2019級即將迎來中考,很多家長都在為孩子準備營養午餐.一家快餐店看準了商機,在5月5號推出了A,B,C三種營養套餐.套餐C單價比套餐A貴5元,三種套餐的單價均為整數,其中A套餐比C套餐少賣12份,B套餐比C套餐少賣6份,且C套餐當天賣出的數量大于26且不超過32,當天總銷售量為偶數且當天銷售額達到了1830元,商家發現C套餐很受歡迎,因此在6號加推出了C套餐升級版D套餐,四種套餐同時售賣,A套餐比5號銷售量減少,C套餐比5號銷售量增加![]() ,且A減少的份數比C套餐增加的份數多5份,B套餐銷售量不變,由于商家人手限制,兩天的總銷售量相同,則其他套餐單價不變的情況下,D套餐至少比C套餐費貴______時,才能使6號銷售額達到1950元.
,且A減少的份數比C套餐增加的份數多5份,B套餐銷售量不變,由于商家人手限制,兩天的總銷售量相同,則其他套餐單價不變的情況下,D套餐至少比C套餐費貴______時,才能使6號銷售額達到1950元.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖4,在梯形ABCD中,AD∥BC,∠BCD=90°,BC=2AD,F,E分別是AB,BC的中點,則下列結論不一定正確的是( )
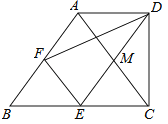
A.△ABC是等腰三角形B.四邊形EFAM是菱形
C.![]() D.DE平分∠CDF
D.DE平分∠CDF
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】對于反比例函數y=![]() ,下列說法不正確的是( )
,下列說法不正確的是( )
A.圖象分布在第一、三象限
B.當x>0時,y隨x的增大而減小
C.圖象經過點(2,3)
D.若點A(x1,y1),B(x2,y2)都在圖象上,且x1<x2,則y1<y2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】兩個一次函數l1、l2的圖象如圖:

(1)分別求出l1、l2兩條直線的函數關系式;
(2)求出兩直線與y軸圍成的△ABP的面積;
(3)觀察圖象:請直接寫出當x滿足什么條件時,l1的圖象在l2的下方.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com