
題目列表(包括答案和解析)
已知向量 (
( ),向量
),向量 ,
, ,
,
且

 .
.
(Ⅰ)求向量 ;
(Ⅱ)若
;
(Ⅱ)若 ,
, ,求
,求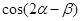 .
.
【解析】本試題主要考查了向量的數(shù)量積的運(yùn)算,以及兩角和差的三角函數(shù)關(guān)系式的運(yùn)用。
(1)問(wèn)中∵ ,∴
,∴ ,…………………1分
,…………………1分
∵ ,得到三角關(guān)系是
,得到三角關(guān)系是 ,結(jié)合
,結(jié)合 ,解得。
,解得。
(2)由 ,解得
,解得 ,
, ,結(jié)合二倍角公式
,結(jié)合二倍角公式 ,和
,和 ,代入到兩角和的三角函數(shù)關(guān)系式中就可以求解得到。
,代入到兩角和的三角函數(shù)關(guān)系式中就可以求解得到。
解析一:(Ⅰ)∵ ,∴
,∴ ,…………1分
,…………1分
∵ ,∴
,∴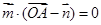 ,即
,即 ① …………2分
① …………2分
又 ② 由①②聯(lián)立方程解得,
② 由①②聯(lián)立方程解得,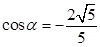 ,
,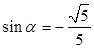 5分
5分
∴ ……………6分
……………6分
(Ⅱ)∵ 即
即 ,
, , …………7分
, …………7分
∴ ,
, ………8分
………8分
又∵ , ………9分
, ………9分
 , ……10分
, ……10分
∴ .
.
解法二: (Ⅰ) ,…………………………………1分
,…………………………………1分
又 ,∴
,∴ ,即
,即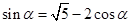 ,①……2分
,①……2分
又 ②
②
將①代入②中,可得 ③ …………………4分
③ …………………4分
將③代入①中,得 ……………………………………5分
……………………………………5分
∴ …………………………………6分
…………………………………6分
(Ⅱ) 方法一
∵ ,
, ,∴
,∴ ,且
,且 ……7分
……7分
∴ ,從而
,從而 . …………………8分
. …………………8分
由(Ⅰ)知 ,
,
 ; ………………9分
; ………………9分
∴ . ………………………………10分
. ………………………………10分
又∵ ,∴
,∴ ,
又
,
又 ,∴
,∴ ……11分
……11分
綜上可得  ………………………………12分
………………………………12分
方法二∵ ,
, ,∴
,∴ ,且
,且 …………7分
…………7分
∴ .
……………8分
.
……………8分
由(Ⅰ)知 ,
, .
…………9分
.
…………9分
∴ ……………10分
……………10分
∵ ,且注意到
,且注意到 ,
,
∴ ,又
,又 ,∴
,∴ ………………………11分
………………………11分
綜上可得  …………………12分
…………………12分
(若用 ,又∵
,又∵ ∴
∴  ,
,
如圖, 是△
是△ 的重心,
的重心, 、
、 分別是邊
分別是邊 、
、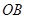 上的動(dòng)點(diǎn),且
上的動(dòng)點(diǎn),且 、
、 、
、 三點(diǎn)共線(xiàn).
三點(diǎn)共線(xiàn).
(1)設(shè)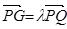 ,將
,將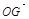 用
用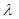 、
、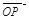 、
、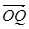 表示;
表示;
(2)設(shè)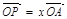 ,
,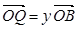 ,證明:
,證明: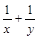 是定值;
是定值;
(3)記△ 與△
與△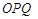 的面積分別為
的面積分別為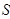 、
、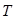 .求
.求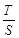 的取值范圍.
的取值范圍.
(提示: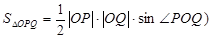
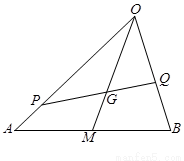
【解析】第一問(wèn)中利用(1)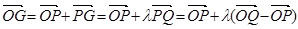
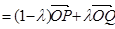
第二問(wèn)中,由(1),得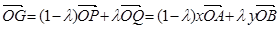 ;①
;①
另一方面,∵ 是△
是△ 的重心,
的重心,
∴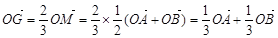
而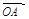 、
、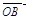 不共線(xiàn),∴由①、②,得
不共線(xiàn),∴由①、②,得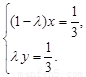
第三問(wèn)中,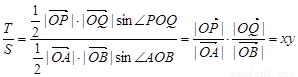
由點(diǎn) 、
、 的定義知
的定義知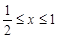 ,
,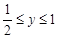 ,
,
且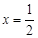 時(shí),
時(shí),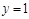 ;
;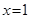 時(shí),
時(shí),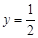 .此時(shí),均有
.此時(shí),均有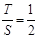 .
.
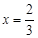 時(shí),
時(shí),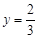 .此時(shí),均有
.此時(shí),均有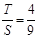 .
.
以下證明: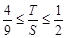 ,結(jié)合作差法得到。
,結(jié)合作差法得到。
解:(1)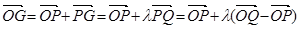
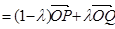 .
.
(2)一方面,由(1),得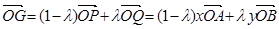 ;①
;①
另一方面,∵ 是△
是△ 的重心,
的重心,
∴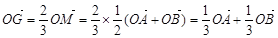 . ②
. ②
而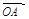 、
、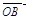 不共線(xiàn),∴由①、②,得
不共線(xiàn),∴由①、②,得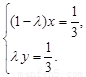
解之,得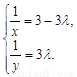 ,∴
,∴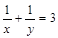 (定值).
(定值).
(3)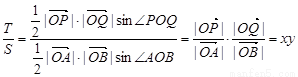 .
.
由點(diǎn) 、
、 的定義知
的定義知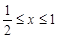 ,
,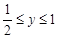 ,
,
且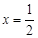 時(shí),
時(shí),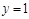 ;
;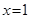 時(shí),
時(shí),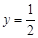 .此時(shí),均有
.此時(shí),均有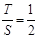 .
.
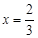 時(shí),
時(shí),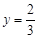 .此時(shí),均有
.此時(shí),均有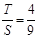 .
.
以下證明: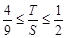 .(法一)由(2)知
.(法一)由(2)知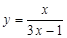 ,
,
∵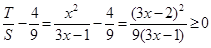 ,∴
,∴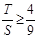 .
.
∵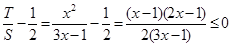 ,∴
,∴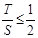 .
.
∴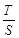 的取值范圍
的取值范圍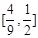
x+
|
y+
|
| ||
| 2 |
| ||
| 3 |
| ||
| 3 |
| C | 0 n |
| C | 1 n |
| C | 2 n |
| C | n n |
| C | 2 n |
| C | 3 n |
| C | 4 n |
| C | n n |
| C | 1 n |
| C | 2 n |
| C | 3 n |
| C | n n |
| C | 2 n |
| C | 3 n |
| C | 4 n |
| C | n n |
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話(huà):027-86699610 舉報(bào)郵箱:58377363@163.com