
2007屆廣東省韶關(guān)市高三摸底考試數(shù)學(xué)(文)試題
本試卷分第Ⅰ卷(選擇題)和第Ⅱ卷(非選擇)題兩部分,滿分150分.考試用時120分鐘.
參考公式:  , 其中
, 其中 是錐體的底面積,
是錐體的底面積, 是錐體的高.
是錐體的高.
一、選擇題(共10小題,每題5分)
1.已知復(fù)數(shù)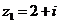 ,
,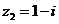 ,則在
,則在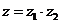 復(fù)平面上對應(yīng)的點位于(
)
復(fù)平面上對應(yīng)的點位于(
)
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
2.有3張獎券,其中2張可中獎,現(xiàn)3個人按順序依次從中抽一張,小明最后抽,則他抽到中獎券的概率是( )
(A)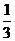 (B)
(B) (C)
(C)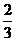 (D)
(D)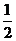
3.已知命題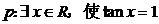 ,命題
,命題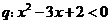 的解集是
的解集是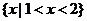 ,下列結(jié)論:
,下列結(jié)論:
①命題“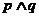 ”是真命題; ②命題“
”是真命題; ②命題“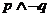 ”是假命題;
”是假命題;
③命題“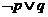 ”是真命題; ④命題“
”是真命題; ④命題“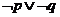 ”是假命題
”是假命題
其中正確的是( )
(A)②③ (B)①②④ (C)①③④ (D)①②③④
4.已知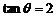 ,則
,則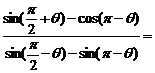 ( )
( )
(A)2 (B)-2 (C)0 (D)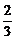
5.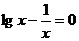 有解的區(qū)域是( )
有解的區(qū)域是( )
(A)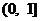 (B)
(B)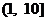 (C)
(C)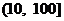 (D)
(D)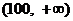
6.已知向量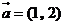 ,
,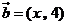 ,若向量
,若向量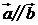 ,則
,則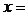 ( )
( )
(A)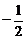 (B)
(B)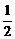 (C)
(C)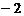 (D)2
(D)2
7.已知兩點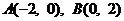 ,點
,點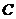 是圓
是圓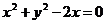 上任意一點,則
上任意一點,則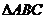 面積的最小值是( )
面積的最小值是( )
(A)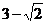 (B)
(B)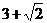 (C)
(C)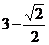 (D)
(D)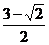
8. 甲、乙、丙、丁四位同學(xué)各自對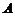 、
、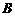 兩變量的線性相關(guān)性作試驗,并用回歸分析方法分別求得相關(guān)系數(shù)
兩變量的線性相關(guān)性作試驗,并用回歸分析方法分別求得相關(guān)系數(shù)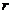 與殘差平方和
與殘差平方和 如下表:
如下表:
甲
乙
丙
丁
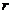
0.82
0.78
0.69
0.85

115
106
124
103
則哪位同學(xué)的試驗結(jié)果體現(xiàn)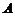 、
、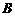 兩變量更強(qiáng)的線性相關(guān)性?( )
兩變量更強(qiáng)的線性相關(guān)性?( )
 甲
甲
 乙
乙
 丙
丙  丁
丁
 9.如圖,一個空間幾何體的主視圖、左視圖、俯視圖為全等的等腰直角三角形,如果直角三角形的直角邊長為1,那么這個幾何體的體積為(
)
9.如圖,一個空間幾何體的主視圖、左視圖、俯視圖為全等的等腰直角三角形,如果直角三角形的直角邊長為1,那么這個幾何體的體積為(
)
(A)1 (B)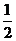
(C)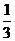 (D)
(D)
10.已知拋物線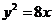 ,過點
,過點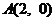 )作傾斜角為
)作傾斜角為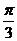 的直線
的直線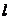 ,若
,若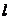 與拋物線交于
與拋物線交于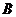 、
、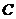 兩點,弦
兩點,弦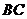 的中垂線交
的中垂線交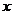 軸于點
軸于點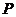 ,則線段
,則線段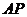 的長為(
)
的長為(
)
(A) (B)
(B)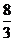 (C)
(C) (D)
(D)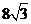
二、填空題(共4小題,每小題5分)
11.已知集合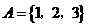 ,使
,使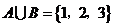 的集合B的個數(shù)是_________.
的集合B的個數(shù)是_________.
12.在約束條件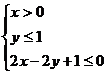 下,目標(biāo)函數(shù)
下,目標(biāo)函數(shù)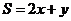 的最大值為_____________.
的最大值為_____________.
13.在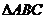 中,若
中,若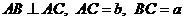 ,則
,則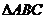 的外接圓半徑
的外接圓半徑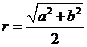 ,將此結(jié)論拓展到空間,可得出的正確結(jié)論是:在四面體
,將此結(jié)論拓展到空間,可得出的正確結(jié)論是:在四面體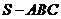 中,若
中,若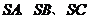 兩兩垂直,
兩兩垂直,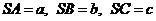 ,則四面體
,則四面體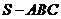 的外接球半徑
的外接球半徑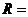 ____________.
____________.
14.在如下程序框圖中,輸入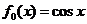 ,則輸出的是__________.
,則輸出的是__________.


三、解答題(共6小題,共80分)
15.(本題滿分12分)在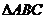 中,
中,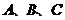 是三角形的三內(nèi)角,
是三角形的三內(nèi)角,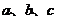 是三內(nèi)角對應(yīng)的三邊,已知
是三內(nèi)角對應(yīng)的三邊,已知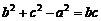 .
.
(Ⅰ)求角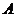 的大小;
的大小;
(Ⅱ)若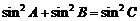 ,求角
,求角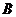 的大小.
的大小.
16.(本題滿分12分)已知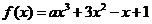 ,
,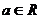 .
.
(Ⅰ)當(dāng)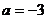 時,求證:
時,求證: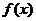 在
在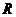 上是減函數(shù);
上是減函數(shù);
(Ⅱ)如果對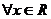 不等式
不等式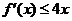 恒成立,求實數(shù)
恒成立,求實數(shù)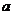 的取值范圍.
的取值范圍.
 17.(本題滿分14分)如圖所示,在棱長為2的正方體
17.(本題滿分14分)如圖所示,在棱長為2的正方體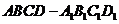 中,
中,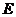 、
、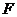 分別為
分別為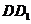 、
、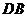 的中點.
的中點.
(Ⅰ)求證: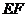 //平面
//平面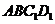 ;
;
(Ⅱ)求證: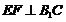 ;
;
(Ⅲ)求三棱錐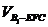 的體積.
的體積.
18.(本題滿分14分)某養(yǎng)殖廠需定期購買飼料,已知該廠每天需要飼料200公斤,每公斤飼料的價格為1.8元,飼料的保管與其他費用為平均每公斤每天0.03元,購買飼料每次支付運費300元.
(Ⅰ)求該廠多少天購買一次飼料才能使平均每天支付的總費用最小;
(Ⅱ)若提供飼料的公司規(guī)定,當(dāng)一次購買飼料不少5噸時其價格可享受八五折優(yōu)惠(即原價的85%).問該廠是否考慮利用此優(yōu)惠條件,請說明理由.
 19.(本題滿分14分)觀察下面由奇數(shù)組成的數(shù)陣,回答下列問題:
19.(本題滿分14分)觀察下面由奇數(shù)組成的數(shù)陣,回答下列問題:
(Ⅰ)求第六行的第一個數(shù).
(Ⅱ)求第20行的第一個數(shù).
(Ⅲ)求第20行的所有數(shù)的和.
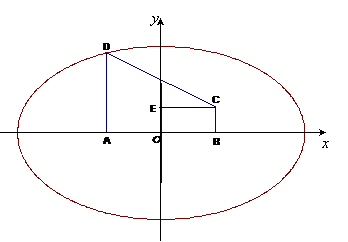
20.(本題滿分14分)如圖,在直角梯形 中,
中,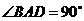 ,
, ,
,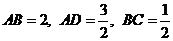 ,橢圓以
,橢圓以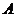 、
、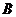 為焦點且經(jīng)過點
為焦點且經(jīng)過點 .
.
(Ⅰ)建立適當(dāng)?shù)闹苯亲鴺?biāo)系,求橢圓的方程;
 (Ⅱ)若點
(Ⅱ)若點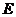 滿足
滿足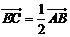 ,問是否存在直線
,問是否存在直線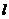 與橢圓交于
與橢圓交于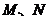 兩點,且
兩點,且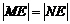 ?若存在,求出直線
?若存在,求出直線 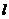 與
與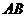 夾角
夾角 的正切值的取值范圍;若不存在,請說明理由.
的正切值的取值范圍;若不存在,請說明理由.
2007屆廣東省韶關(guān)市高三摸底考試數(shù)學(xué)(文)試題
答案及評分標(biāo)準(zhǔn)
DCDBB DADDA
題號
11
12
13
14
答案
8
2
二、填空題

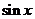
三、解答題
15.解:(Ⅰ)在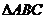 中,
中,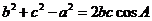 且
且 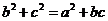
 ,
, …………6分
…………6分
(Ⅱ)由正弦定理,又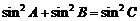 ,故
,故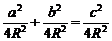 …………8分
…………8分
即: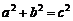 故
故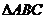 是以
是以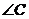 為直角的直角三角形……………10分
為直角的直角三角形……………10分
又∵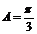 , ∴
, ∴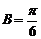 …………………………12分
…………………………12分
16.解:(Ⅰ)當(dāng)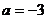 時,
時,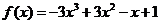 ……………1分
……………1分
∵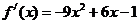 ………………2分
………………2分
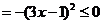 ……………3分
……………3分
∴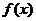 在
在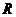 上是減函數(shù) …………4分
上是減函數(shù) …………4分
(Ⅱ)∵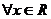 不等式
不等式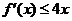 恒成立
恒成立
即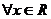 不等式
不等式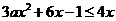 恒成立
恒成立
∴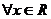 不等式
不等式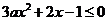 恒成立 …………………6分
恒成立 …………………6分
當(dāng)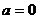 時,
時,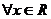
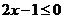 不恒成立 ……………7分
不恒成立 ……………7分
當(dāng)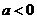 時,
時,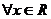 不等式
不等式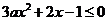 恒成立 ……………8分
恒成立 ……………8分
即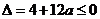
∴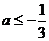 …………………10分
…………………10分
當(dāng)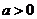 時,
時,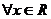 不等式
不等式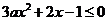 不恒成立… … …… 11分
不恒成立… … …… 11分
綜上所述,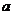 的取值范圍是
的取值范圍是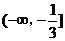 … … … …12分
… … … …12分
17.證明:(Ⅰ)連結(jié)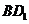 ,在
,在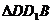 中,
中,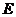 、
、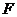 分別為
分別為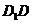 ,
,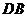 的中點,則
的中點,則

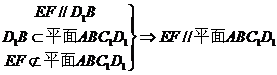 ……………4分
……………4分
(Ⅱ)
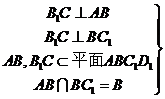
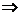
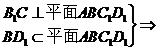

 …………9分
…………9分
(Ⅲ)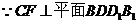
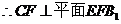 且
且 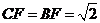
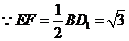 ,
,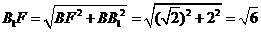 ………10分
………10分
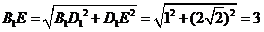
∴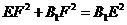
即 …………………12分
…………………12分
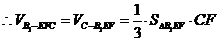 =
=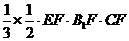
=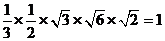 ………………14分
………………14分
18.解:(Ⅰ)設(shè)該廠應(yīng)隔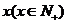 天購買一次飼料,平均每天支付的總費用為
天購買一次飼料,平均每天支付的總費用為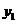 …1分
…1分
∵飼料的保管與其它費用每天比前一天少200×0.03=6(元),
∴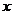 天飼料的保管與其它費用共是
天飼料的保管與其它費用共是
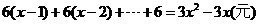 ………………4分
………………4分
從而有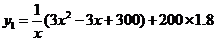 …………5分
…………5分
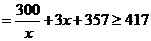 ………………7分
………………7分
當(dāng)且僅當(dāng)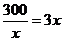 ,即
,即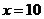 時,
時,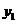 有最小值………………8分
有最小值………………8分
即每隔10天購買一次飼料才能使平均每天支付的總費用最小.
(Ⅱ)若廠家利用此優(yōu)惠條件,則至少25天購買一次飼料,設(shè)該廠利用此優(yōu)惠條件,每隔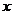 天(
天(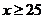 )購買一次飼料,平均每天支付的總費用為
)購買一次飼料,平均每天支付的總費用為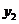 ,則
,則
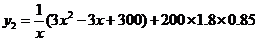
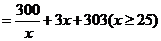 ……………10分
……………10分
∵
∴當(dāng)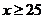 時,
時, ,即函數(shù)
,即函數(shù)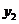 在
在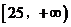 上是增函數(shù)…………12分
上是增函數(shù)…………12分
∴當(dāng)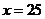 時,
時,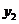 取得最小值為
取得最小值為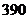 ,而
,而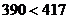 ……………13分
……………13分
∴該廠應(yīng)接受此優(yōu)惠條件 ……………14分
19.解:(Ⅰ)第六行的第一個數(shù)為31 ……………2分
(Ⅱ)∵第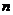 行的最后一個數(shù)是
行的最后一個數(shù)是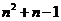 ,第
,第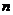 行共有
行共有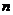 個數(shù),且這些數(shù)構(gòu)成一個等差數(shù)列,設(shè)第
個數(shù),且這些數(shù)構(gòu)成一個等差數(shù)列,設(shè)第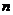 行的第一個數(shù)是
行的第一個數(shù)是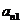 ……………5分
……………5分
∴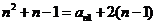 ……………7分
……………7分
∴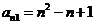 …………9分
…………9分
∴第20行的第一個數(shù)為381 ……………10分
(Ⅲ)第20行構(gòu)成首項為381,公差為2的等差數(shù)列,且有20個數(shù)
設(shè)第20行的所有數(shù)的和為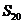 ………………12分
………………12分
則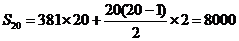 ……………14分
……………14分
20.解:(Ⅰ)如圖,以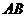 所在直線為
所在直線為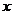 軸,
軸,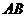 的垂直平分線為
的垂直平分線為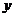 軸建立直角坐標(biāo)系
軸建立直角坐標(biāo)系
則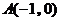 ,
,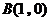 ,
,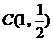 ,
, ………2分
………2分
 設(shè)橢圓方程為
設(shè)橢圓方程為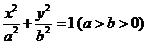
則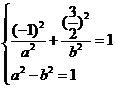
解得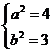 ………………4分
………………4分
∴所求橢圓方程為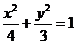 …………………5分
…………………5分
(Ⅱ)由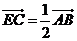 得點
得點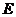 的坐標(biāo)為
的坐標(biāo)為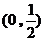
顯然直線 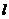 與
與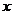 軸平行時滿足題意,即
軸平行時滿足題意,即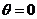 …………6分
…………6分
直線 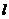 與
與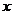 軸垂直時不滿足題意
軸垂直時不滿足題意
不妨設(shè)直線 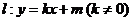 ……………7分
……………7分
由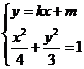 得
得 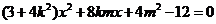 ………9分
………9分
由 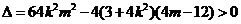 得
得 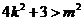 ………10分
………10分
設(shè)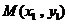 ,
,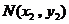 ,
,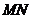 的中點為
的中點為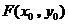
則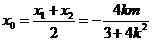 ,
,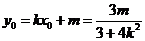 ………11分
………11分
∵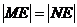
∴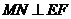
∴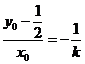 即
即 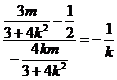
解得: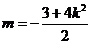 ………………12分
………………12分
由 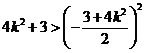 得
得 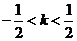 且
且 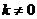 …………13分
…………13分
故直線 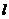 與
與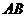 夾角
夾角 的正切值的取值范圍是
的正切值的取值范圍是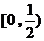 ……………14分
……………14分
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com