
��Ŀ�� ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ij�Г�(j��)��(sh��)�H��r��Ҫ��ȡ�����ķN��ؚ��ʽ����һ���Թ����c��ʽ��ָ����Ͷ�Y���O(sh��)���A(ch��)�O(sh��)ʩ���̣��M��ؚ���^(q��)Ⱥ�����ӹ��̽��O(sh��)���@�Äڄ�(w��)��(b��o)�꣬�ڶ����������M(j��n)��ʽָ��ؚ�������w�ͷ���(du��)�ͷ���(du��)�ڵ��壬�Y���ŵ��壬��ؚЧ�浽��(h��)���������Ƽ���ؚ��ʽ��ָ�M���Ƽ��ˆT����ؚ���l(xi��ng)�匍(sh��)��ָ��(d��o)�����g(sh��)��Ӗ(x��n)�Ȃ��ڿƼ�֪�R(sh��)�����ģ�������w��ʽ��ָ��(du��)Ŀǰ�O�ٔ�(sh��)��ס������l�����ӡ���Ȼ�YԴؚ���^(q��)�������˿ڣ���(sh��)����Ը����ԓ�О���2020����õ���ɾ���(zh��n)��ؚ���(xi��ng)�΄�(w��)��2020�����ȫ��ؚ����(h��)����һ��ؚ����(h��)������������(h��)���(l��i)�����S�C(j��)��ȡ��5000��(h��)��Ŀǰ����Ҫ�ķN��ؚ��ʽ���ˆ�(w��n)���{(di��o)�飬֧��ÿ�N��ؚ��ʽ�ĽY(ji��)�������
�{(di��o)���ؚ����(h��) | ֧���Թ����c��(h��)��(sh��) | ֧���������M(j��n)��(h��)��(sh��) | ֧�ֿƼ���ؚ��(h��)��(sh��) | ֧��������w��(h��)��(sh��) |
һ��ؚ����(h��) | 1200 | 1600 |
| 200 |
���ؑ�(h��)���屣��(h��)��������(h��)�� | 100 |
|
| 100 |
��֪�ڱ��{(di��o)���5000��(h��)���S�C(j��)��ȡһ��(h��)֧���������M(j��n)�ĸ��ʞ�0.36.
���F(xi��n)�÷ӳ�ӵķ��������Ѕ��c�{(di��o)���ؚ����(h��)�г�ȡ50��(h��)�M(j��n)�������LՄ����(w��n)��(y��ng)��֧�ֿƼ���ؚ��(h��)��(sh��)�г�ȡ���ّ�(h��)��
�����mȻ����������(h��)��ȫ�е�ؚ����(h��)��ռ�������������{(di��o)��Ҫ�����x�������@���{(di��o)�������������(h��)��(h��)��(sh��)���ܵ��ڱ��{(di��o)�鿂��(h��)��(sh��)��9.2%����֪![]() �����{(di��o)�������x�ĸ����Ƕ��٣�
�����{(di��o)�������x�ĸ����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ�� ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�E�A![]() �^(gu��)�c(di��n)
�^(gu��)�c(di��n)![]() �ҙE�A�Ķ��S�L(zh��ng)��
�ҙE�A�Ķ��S�L(zh��ng)��![]() .
.
������E�A![]() �ķ��̣�
�ķ��̣�
������֪?ji��ng)�ֱ��(xi��n)![]() �^(gu��)�ҽ��c(di��n)
�^(gu��)�ҽ��c(di��n)![]() �����c�E�A
�����c�E�A![]() �քe����
�քe����![]() ���c(di��n).ԇ��(w��n)
���c(di��n).ԇ��(w��n)![]() �S���Ƿ���ڶ��c(di��n)
�S���Ƿ���ڶ��c(di��n)![]() ��ʹ�ã�
��ʹ�ã�![]() �����������������c(di��n)
�����������������c(di��n)![]() ������(bi��o)���������ڣ��f(shu��)������.
������(bi��o)���������ڣ��f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�� ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ֱ������(bi��o)ϵ![]() �У�ֱ��(xi��n)
�У�ֱ��(xi��n)![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�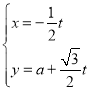 ��
��![]() �酢��(sh��)��
�酢��(sh��)��![]() ��.������(bi��o)ԭ�c(di��n)��O�c(di��n)��
��.������(bi��o)ԭ�c(di��n)��O�c(di��n)��![]() �S�����S��O�S�����O����(bi��o)ϵ������(xi��n)
�S�����S��O�S�����O����(bi��o)ϵ������(xi��n)![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() ���侀(xi��n)
���侀(xi��n)![]() �c����(xi��n)
�c����(xi��n)![]() ����
����![]() ���c(di��n)��ֱ��(xi��n)
���c(di��n)��ֱ��(xi��n)![]() �c����(xi��n)
�c����(xi��n)![]() �ཻ��
�ཻ��![]() ���c(di��n).
���c(di��n).
������ֱ��(xi��n)![]() ����ͨ���̺�����(xi��n)C��ֱ������(bi��o)���̣�
����ͨ���̺�����(xi��n)C��ֱ������(bi��o)���̣�
����(d��ng)![]() �r(sh��)����
�r(sh��)����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�� ��(l��i)Դ�� �}�ͣ�
���}Ŀ�����������ď���Ƭ���քe��(xi��)�����W(xu��)����(x��)����(qi��ng)����(gu��)���Ă�(g��)�֣��зŻص؏�����ȡһ����Ƭ�������γ�ȡ�W(xu��)������(x��)���ɂ�(g��)�ֶ�ȡ��ӛ���¼�![]() �����S�C(j��)ģ�M�ķ�����Ӌ(j��)�¼�
�����S�C(j��)ģ�M�ķ�����Ӌ(j��)�¼�![]() �l(f��)���ĸ��ʣ�������X�S�C(j��)�a(ch��n)������(sh��)0��1��2��3�Ă�(g��)�S�C(j��)��(sh��)���քe�������W(xu��)����(x��)����(qi��ng)����(gu��)���@�Ă�(g��)�֣���ÿ����(g��)�S�C(j��)��(sh��)��һ�M����ʾȡ��Ƭ���εĽY(ji��)������(j��ng)�S�C(j��)ģ�M�a(ch��n)��������18�M�S�C(j��)��(sh��)��
�l(f��)���ĸ��ʣ�������X�S�C(j��)�a(ch��n)������(sh��)0��1��2��3�Ă�(g��)�S�C(j��)��(sh��)���քe�������W(xu��)����(x��)����(qi��ng)����(gu��)���@�Ă�(g��)�֣���ÿ����(g��)�S�C(j��)��(sh��)��һ�M����ʾȡ��Ƭ���εĽY(ji��)������(j��ng)�S�C(j��)ģ�M�a(ch��n)��������18�M�S�C(j��)��(sh��)��
232 | 321 | 210 | 023 | 123 | 021 | 132 | 220 | 001 |
231 | 130 | 133 | 231 | 031 | 320 | 122 | 103 | 233 |
�ɴ˿��Թ�Ӌ(j��)�¼�![]() �l(f��)���ĸ��ʞ飨 ��
�l(f��)���ĸ��ʞ飨 ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ�� ��(l��i)Դ�� �}�ͣ�
���}Ŀ���҅^(q��)����С�W(xu��)�k�W(xu��)�l���������Ľ�������(d��o)�£�Ѹ�ٵõ���׃.����(d��o)һ���.�քe�S�C(j��)����˸��У���![]() ��ʾ���c���У���
��ʾ���c���У���![]() ��ʾ����10���W(xu��)У.�õ����P(gu��n)ָ��(bi��o)�ľC���u(p��ng)�r(ji��)�÷֣��ٷ��ƣ����o�~�D��D��ʾ.�t���o�~�D�ɵó����_����Ϣ�飨80�ּ����Ϟ郞(y��u)�㣩�� ��
��ʾ����10���W(xu��)У.�õ����P(gu��n)ָ��(bi��o)�ľC���u(p��ng)�r(ji��)�÷֣��ٷ��ƣ����o�~�D��D��ʾ.�t���o�~�D�ɵó����_����Ϣ�飨80�ּ����Ϟ郞(y��u)�㣩�� ��
�ٸ��е÷��c���е÷ֵă�(y��u)������ͬ
�ڸ��е÷��c���е÷ֵ���λ��(sh��)��ͬ
�۸��е÷ֵķ���ȳ��е÷ֵķ����
�ܸ��е÷��c���е÷ֵ�ƽ������ͬ
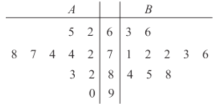
A.�٢�B.�٢�C.�ڢ�D.�ۢ�
�鿴�𰸺ͽ���>>
��Ŀ�� ��(l��i)Դ�� �}�ͣ�
���}Ŀ����D��������![]() �Ă�(c��)��
�Ă�(c��)��![]() ��ֱ�ڵ���
��ֱ�ڵ���![]() ����
����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ����
����![]() �����c(di��n).
�����c(di��n).
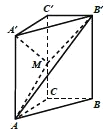
��1���C����![]() ��
��
��2��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�� ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪![]() ��
��![]() ����(d��ng)�c(di��n)
����(d��ng)�c(di��n)![]() �M(m��n)��ֱ��(xi��n)
�M(m��n)��ֱ��(xi��n)![]() �cֱ��(xi��n)
�cֱ��(xi��n)![]() ��б��֮�e��
��б��֮�e��![]() ���O(sh��)�c(di��n)
���O(sh��)�c(di��n)![]() ��܉�E������(xi��n)
��܉�E������(xi��n)![]() .
.
��1��������(xi��n)![]() �ķ��̣�
�ķ��̣�
��2�����^(gu��)�c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �c����(xi��n)
�c����(xi��n)![]() ����
����![]() ��
��![]() ���c(di��n)���^(gu��)�c(di��n)
���c(di��n)���^(gu��)�c(di��n)![]() ���cֱ��(xi��n)
���cֱ��(xi��n)![]() ��ֱ��ֱ��(xi��n)�c
��ֱ��ֱ��(xi��n)�c![]() �ཻ���c(di��n)
�ཻ���c(di��n)![]() ����
����![]() ����Сֵ���˕r(sh��)ֱ��(xi��n)
����Сֵ���˕r(sh��)ֱ��(xi��n)![]() �ķ���.
�ķ���.
�鿴�𰸺ͽ���>>
��Ŀ�� ��(l��i)Դ�� �}�ͣ�
���}Ŀ���@���¹ڷ������飬�����Ї�(gu��)�����ԁ�(l��i)���҇�(gu��)�l(f��)���Ă����ٶ���졢��Ⱦ������V�������y������һ���ش�ͻ�l(f��)�����l(w��i)���¼�.���A����vʷ�Ͻ�(j��ng)�v�^(gu��)�ܶ�ĥ�y�����ā�(l��i)�](m��i)�б������^(gu��)�������������£�������ĥ�y�г��L(zh��ng)����ĥ�y�Њ^��.���@�������У�ȫ��(gu��)����չ�F(xi��n)������؟(z��)�Γ�(d��n)��(d��ng)֮�¡����пƌW(xu��)����֮��.ijУ�����W(xu��)��Ҳչ�_(k��i)�ˌ�(du��)�@��������о���һ��ͬ�W(xu��)�ڔ�(sh��)��(j��)�y(t��ng)Ӌ(j��)�аl(f��)�F(xi��n)����2020��2��1����2��7�����g������![]() ��ȫ��(gu��)��Ӌ(j��)��(b��o)��_�\������(sh��)��
��ȫ��(gu��)��Ӌ(j��)��(b��o)��_�\������(sh��)��![]() ����λ���f(w��n)�ˣ�֮�g���P(gu��n)ϵ���±���
����λ���f(w��n)�ˣ�֮�g���P(gu��n)ϵ���±���
���� | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
ȫ��(gu��)��Ӌ(j��)��(b��o)��_�\������(sh��)�� | 1.4 | 1.7 | 2.0 | 2.4 | 2.8 | 3.1 | 3.5 |
��1������(j��)���еĔ�(sh��)��(j��)���\(y��n)�����P(gu��n)ϵ��(sh��)�M(j��n)�з����f(shu��)�����Ƿ�����þ�(xi��n)�Իؚwģ�͔M��![]() �c
�c![]() ���P(gu��n)ϵ��
���P(gu��n)ϵ��
��2�����![]() �P(gu��n)��
�P(gu��n)��![]() �ľ�(xi��n)�Իؚw����
�ľ�(xi��n)�Իؚw����![]() ��ϵ��(sh��)���_��0.01��.���A(y��)�y(c��)2��10��ȫ��(gu��)��Ӌ(j��)��(b��o)��_�\������(sh��).
��ϵ��(sh��)���_��0.01��.���A(y��)�y(c��)2��10��ȫ��(gu��)��Ӌ(j��)��(b��o)��_�\������(sh��).
������(sh��)��(j��)��![]() ��
��![]() ��
�� ��
��![]() .
.
������ʽ�����P(gu��n)ϵ��(sh��)
�ؚw����![]() ��б�ʺͽؾ����С���˹�Ӌ(j��)��ʽ�քe�飺
��б�ʺͽؾ����С���˹�Ӌ(j��)��ʽ�քe�飺
 ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�� ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() ,ʹ�Ì�(du��)����ɂ�(g��)���ȵ�����(sh��)��(sh��)
,ʹ�Ì�(du��)����ɂ�(g��)���ȵ�����(sh��)��(sh��)![]() ������
������![]() �����.
�����.
��1����![]() �Ľ���ʽ��
�Ľ���ʽ��
��2��������![]() �Ѓɂ�(g��)��(sh��)��
�Ѓɂ�(g��)��(sh��)��![]() ����
����![]() �����C��
�����C��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ�� ��(l��i)Դ�� �}�ͣ�
���}Ŀ��ijؚ���^(q��)�ׂ�(g��)���������Ѓɗl���ֱ��ֱ��(xi��n)��·![]() ���Լ��F·��(xi��n)�ϵ�һ�l��(y��ng)�_(k��i)菵�ֱ��(xi��n)��ɽ����
���Լ��F·��(xi��n)�ϵ�һ�l��(y��ng)�_(k��i)菵�ֱ��(xi��n)��ɽ����![]() �����M(j��n)һ������ɽ�^(q��)�Ľ�ͨ�F(xi��n)�Ӌ(j��)����һ�l�B�Ӄɗl��·
�����M(j��n)һ������ɽ�^(q��)�Ľ�ͨ�F(xi��n)�Ӌ(j��)����һ�l�B�Ӄɗl��·![]() ��ɽ�^(q��)߅���ֱ��(xi��n)��·
��ɽ�^(q��)߅���ֱ��(xi��n)��·![]() �� ��
�� ��![]() ���ڵ�ֱ��(xi��n)�քe��
���ڵ�ֱ��(xi��n)�քe��![]() �S��
�S��![]() �S�� ����ƽ��ֱ������(bi��o)ϵ
�S�� ����ƽ��ֱ������(bi��o)ϵ![]() �� ��D��ʾ�� ɽ�^(q��)߅������(xi��n)��
�� ��D��ʾ�� ɽ�^(q��)߅������(xi��n)��![]() ���O(sh��)��·
���O(sh��)��·![]() �c����(xi��n)
�c����(xi��n)![]() �������c(di��n)
�������c(di��n)![]() ��
��![]() �ęM����(bi��o)��
�ęM����(bi��o)��![]() .
.
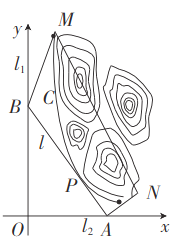
��1����(d��ng)![]() ���ֵ�r(sh��)����·
���ֵ�r(sh��)����·![]() ���L(zh��ng)�����?�������L(zh��ng)�ȣ�
���L(zh��ng)�����?�������L(zh��ng)�ȣ�
��2����(d��ng)��·![]() ���L(zh��ng)����̕r(sh��)���O(sh��)��·
���L(zh��ng)����̕r(sh��)���O(sh��)��·![]() ��
��![]() �S��
�S��![]() �S�քe��
�S�քe��![]() ��
��![]() ���c(di��n)�����y(c��)����߅��
���c(di��n)�����y(c��)����߅��![]() �У�
��![]() ��
��![]() ��
��![]() ǧ�ף�
ǧ�ף�![]() ǧ�ף���(y��ng)�_(k��i)菵�����
ǧ�ף���(y��ng)�_(k��i)菵�����![]() ���L(zh��ng)��.
���L(zh��ng)��.
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com