
【題目】已知數(shù)列![]() 中,
中,![]() ,對任意的
,對任意的![]() ,
,![]() ,有
,有![]() .
.
(1)求數(shù)列![]() 的通項公式;
的通項公式;
(2)設數(shù)列![]() 滿足
滿足![]() (
(![]() ,
,![]() ),
),
①求數(shù)列![]() 的前
的前![]() 項和
項和![]() ;
;
②設![]() 是正整數(shù),若存在正數(shù)
是正整數(shù),若存在正數(shù)![]() ,對任意的正整數(shù)
,對任意的正整數(shù)![]() ,當
,當![]() 時,都有
時,都有![]() ,求m的最大值.
,求m的最大值.
【答案】(1)![]() (2)答案不唯一,具體見解析(3)
(2)答案不唯一,具體見解析(3)![]() 的最大值為5
的最大值為5
【解析】
(1)先證明![]() 是首項,公差都為1的等差數(shù)列,再寫出數(shù)列的通項;(2)①先求出
是首項,公差都為1的等差數(shù)列,再寫出數(shù)列的通項;(2)①先求出![]() ,(
,(![]() ),再分類討論求出數(shù)列
),再分類討論求出數(shù)列![]() 的前
的前![]() 項和
項和![]() ;②原題等價于存在正數(shù)
;②原題等價于存在正數(shù)![]() ,對任意的正整數(shù)
,對任意的正整數(shù)![]() (
(![]() ),當
),當![]() 時,都有
時,都有![]() ,再對
,再對![]() 分類討論求出m的最大值.
分類討論求出m的最大值.
(1)由![]() ,
,![]() ,令
,令![]() ,
,
則![]() ,所以
,所以![]() 是首項,公差都為1的等差數(shù)列,
是首項,公差都為1的等差數(shù)列,
所以![]() 的通項公式為
的通項公式為![]() .
.
(2)由題意![]() ,
,
![]() (
(![]() ),
),
兩式相減得![]() (
(![]() ),
),![]() ,(
,(![]() ),
),
當![]() 時,
時,![]() 滿足上式,所以
滿足上式,所以![]() ,(
,(![]() ).
).
所以①![]() 時,
時,![]() ,
,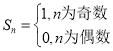 ;
;
②![]() 時,
時,![]() ,
,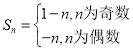
③![]() 且
且![]() 時,
時,![]() ,
,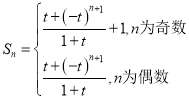 .
.
(3)![]() 等價于
等價于![]() ,
,![]() ,
,
原題等價于存在正數(shù)![]() ,對任意的正整數(shù)
,對任意的正整數(shù)![]() (
(![]() ),當
),當![]() 時,都有
時,都有![]() ,
,
①當![]() 時,
時,![]() ,與題目要求不符;
,與題目要求不符;
②當![]() 時,
時,![]() ,與題目要求不符;
,與題目要求不符;
③當![]() 時,當
時,當![]() 時,上式取對數(shù)得
時,上式取對數(shù)得![]() ,
,
等價于![]() ,
,
設![]() ,
,![]() ,則
,則![]() ,
,
![]() ,
,![]() ,
,![]() 單調遞增;
單調遞增;
![]() ,
,![]() ,
,![]() 單調遞減;
單調遞減;
所以![]() 在
在![]() 取最大值,
取最大值,
又因為![]() ,所以
,所以![]() ;
;
設![]() ,
,![]() ,則
,則 ,
,
設![]() ,
,![]() ,
,![]() ,
,![]() 時
時![]() ,所以
,所以![]() 在
在![]() 遞減,
遞減,
又![]() ,所以
,所以![]() 在
在![]() 恒成立,即
恒成立,即![]() 在
在![]() 遞減.
遞減.
![]() 時,
時,![]() ,
,![]() 存在;
存在;
![]() 時,
時,![]() ,
,![]() 遞減,
遞減,
![]() ,
,![]() ,
,
所以![]() 的最大值為5.
的最大值為5.


科目:高中數(shù)學 來源: 題型:
【題目】第十一屆全國少數(shù)民族傳統(tǒng)體育運動會在河南鄭州舉行,某項目比賽期間需要安排3名志愿者完成5項工作,每人至少完成一項,每項工作由一人完成,則不同的安排方式共有多少種
A.60B.90C.120D.150
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某種水箱用的“浮球”是由兩個相同半球和一個圓柱筒組成,它的軸截面如圖所示,已知半球的直徑是![]() ,圓柱筒高
,圓柱筒高![]() ,為增強該“浮球”的牢固性,給“浮球”內(nèi)置一“雙蝶形”防壓卡,防壓卡由金屬材料桿
,為增強該“浮球”的牢固性,給“浮球”內(nèi)置一“雙蝶形”防壓卡,防壓卡由金屬材料桿![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 及
及![]() 焊接而成,其中
焊接而成,其中![]() ,
,![]() 分別是圓柱上下底面的圓心,
分別是圓柱上下底面的圓心,![]() ,
,![]() ,
,![]() ,
,![]() 均在“浮球”的內(nèi)壁上,AC,BD通過“浮球”中心
均在“浮球”的內(nèi)壁上,AC,BD通過“浮球”中心![]() ,且
,且![]() 、
、![]() 均與圓柱的底面垂直.
均與圓柱的底面垂直.
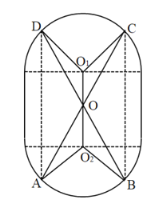
(1)設![]() 與圓柱底面所成的角為
與圓柱底面所成的角為![]() ,試用
,試用![]() 表示出防壓卡中四邊形
表示出防壓卡中四邊形![]() 的面積
的面積![]() ,并寫出
,并寫出![]() 的取值范圍;
的取值范圍;
(2)研究表明,四邊形![]() 的面積越大,“浮球”防壓性越強,求四邊形
的面積越大,“浮球”防壓性越強,求四邊形![]() 面積取最大值時,點
面積取最大值時,點![]() 到圓柱上底面的距離
到圓柱上底面的距離![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,平面ABCD平面PAD,
中,平面ABCD平面PAD,![]() ,
,![]() ,
,![]() ,
,![]() ,E是PD的中點.
,E是PD的中點.

![]() 證明:
證明:![]() ;
;
![]() 設
設![]() ,點M在線段PC上且異面直線BM與CE所成角的余弦值為
,點M在線段PC上且異面直線BM與CE所成角的余弦值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() 的部分圖象如圖所示.
的部分圖象如圖所示.
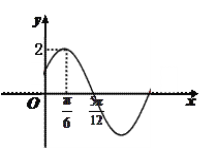
(1) 求函數(shù)![]() 的解析式;
的解析式;
(2) 如何由函數(shù)![]() 的通過適當圖象的變換得到函數(shù)
的通過適當圖象的變換得到函數(shù)![]() 的圖象, 寫出變換過程;
的圖象, 寫出變換過程;
(3) 若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】設![]() ,函數(shù)
,函數(shù)![]() .
.
(1)當![]() 時,求函數(shù)
時,求函數(shù)![]() 的單調區(qū)間;
的單調區(qū)間;
(2)若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上有唯一零點,試求a的值.
上有唯一零點,試求a的值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() (
(![]() ,
,![]() 是自然對數(shù)的底數(shù)).
是自然對數(shù)的底數(shù)).
(1)若函數(shù)![]() 在點
在點![]() 處的切線方程為
處的切線方程為![]() ,試確定函數(shù)
,試確定函數(shù)![]() 的單調區(qū)間;
的單調區(qū)間;
(2)①當![]() ,
,![]() 時,若對于任意
時,若對于任意![]() ,都有
,都有![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的最小值;②當
的最小值;②當![]() 時,設函數(shù)
時,設函數(shù)![]() ,是否存在實數(shù)
,是否存在實數(shù)![]() ,使得
,使得![]() ?若存在,求出
?若存在,求出![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數(shù)方程為
的參數(shù)方程為![]() (
(![]() ,
,![]() 為參數(shù)),以坐標原點
為參數(shù)),以坐標原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的坐標方程為
的坐標方程為![]() ,若直線
,若直線![]() 與曲線
與曲線![]() 相切.
相切.
(1)求曲線![]() 的極坐標方程;
的極坐標方程;
(2)在曲線![]() 上取兩點
上取兩點![]() 、
、![]() 于原點
于原點![]() 構成
構成![]() ,且滿足
,且滿足![]() ,求面積
,求面積![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】在直角坐標系![]() 中,圓
中,圓![]() 的參數(shù)方程
的參數(shù)方程![]() (
(![]() 為參數(shù)).以
為參數(shù)).以![]() 為極點,
為極點,![]() 軸的非負半軸為極軸建立極坐標系.
軸的非負半軸為極軸建立極坐標系.
(1)求圓![]() 的極坐標方程;
的極坐標方程;
(2)直線![]() 的極坐標方程是
的極坐標方程是![]() ,射線
,射線![]() 與圓
與圓![]() 的交點為
的交點為![]() ,
,![]() ,與直線
,與直線![]() 的交點為
的交點為![]() ,求線段
,求線段![]() 的長.
的長.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com