
【題目】△ABC的內角A,B,C的對邊分別為a,b,c,已知2cosC(acosB+bcosA)=c.
(1)求C;
(2)若c= ![]() ,△ABC的面積為
,△ABC的面積為 ![]() ,求△ABC的周長.
,求△ABC的周長.
【答案】
(1)解:已知等式利用正弦定理化簡得:2cosC(sinAcosB+sinBcosA)=sinC,
整理得:2cosCsin(A+B)=sinC,
∵sinC≠0,sin(A+B)=sinC
∴cosC= ![]() ,
,
又0<C<π,
∴C= ![]() ;
;
(2)解:由余弦定理得7=a2+b2﹣2ab ![]() ,
,
∴(a+b)2﹣3ab=7,
∵S= ![]() absinC=
absinC= ![]() ab=
ab= ![]() ,
,
∴ab=6,
∴(a+b)2﹣18=7,
∴a+b=5,
∴△ABC的周長為5+ ![]() .
.
【解析】(1)已知等式利用正弦定理化簡,整理后利用兩角和與差的正弦函數公式及誘導公式化簡,根據sinC不為0求出cosC的值,即可確定出出C的度數;(2)利用余弦定理列出關系式,利用三角形面積公式列出關系式,求出a+b的值,即可求△ABC的周長.


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]()
(1)判斷函數的奇偶性,并加以證明;
(2)用定義證明![]() 在
在![]() 上是減函數;
上是減函數;
(3)函數![]() 在
在![]() 上是單調增函數還是單調減函數?(直接寫出答案,不要求寫證明過程).
上是單調增函數還是單調減函數?(直接寫出答案,不要求寫證明過程).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某貧困地區有1500戶居民,其中平原地區1050戶,山區450戶,為調查該地區2017年家庭收入情況,從而更好地實施“精準扶貧”,采用分層抽樣的方法,收集了150戶家庭2017年年收入的樣本數據(單位:萬元)
(I)應收集多少戶山區家庭的樣本數據?
(Ⅱ)根據這150個樣本數據,得到2017年家庭收入的頻率分布直方圖(如圖所示),其中樣本數據分組區間為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .如果將頻率率視為概率,估計該地區2017年家庭收入超過1.5萬元的概率;
.如果將頻率率視為概率,估計該地區2017年家庭收入超過1.5萬元的概率;
(Ⅲ)樣本數據中,由5戶山區家庭的年收入超過2萬元,請完成2017年家庭收入與地區的列聯表,并判斷是否有90%的把握認為“該地區2017年家庭年收入與地區有關”?
附:![]()
| 0.100 | 0.050 | 0.010 | 0.001 |
| 2.706 | 3.841 | 6.635 | 10.828 |
超過2萬元 | 不超過2萬元 | 總計 | |
平原地區 | |||
山區 | 5 | ||
總計 |

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知符號函數sgnx= 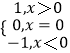 ,f(x)是R上的增函數,g(x)=f(x)﹣f(ax)(a>1),則( )
,f(x)是R上的增函數,g(x)=f(x)﹣f(ax)(a>1),則( )
A.sgn[g(x)]=sgnx
B.sgn[g(x)]=﹣sgnx
C.sgn[g(x)]=sgn[f(x)]
D.sgn[g(x)]=﹣sgn[f(x)]
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知命題:①函數![]() 的值域是
的值域是![]() ;
;
②為了得到函數![]() 的圖象,只需把函數
的圖象,只需把函數![]() 圖象上的所有點向右平移
圖象上的所有點向右平移![]() 個單位長度;
個單位長度;
③當![]() 或
或![]() 時,冪函數
時,冪函數![]() 的圖象都是一條直線;
的圖象都是一條直線;
④已知函數 ,若
,若![]() 互不相等,且
互不相等,且![]() ,則
,則![]() 的取值范圍是
的取值范圍是![]() .
.
其中正確的命題個數為( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出下列四個五個命題:
①“![]() ”是“
”是“![]() ”的充要條件
”的充要條件
②對于命題![]() ,使得
,使得![]() ,則
,則![]() ,均有
,均有![]() ;
;
③命題“若![]() ,則方程
,則方程![]() 有實數根”的逆否命題為:“若方程
有實數根”的逆否命題為:“若方程![]()
![]() 沒有實數根,則
沒有實數根,則![]() ”;
”;
④函數![]() 只有
只有![]() 個零點;
個零點;
⑤![]() 使
使![]() 是冪函數,且在
是冪函數,且在![]() 上單調遞減.
上單調遞減.
其中是真命題的個數為:
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某地合作農場的果園進入盛果期,果農利用互聯網電商渠道銷售蘋果,蘋果單果直徑不同則單價不同,為了更好的銷售,現從該合作農場果園的蘋果樹上隨機摘下了50個蘋果測量其直徑,經統計,其單果直徑分布在區間![]() 內(單位:
內(單位:![]() ),統計的莖葉圖如圖所示:
),統計的莖葉圖如圖所示:

(Ⅰ)按分層抽樣的方法從單果直徑落在![]() ,
,![]() 的蘋果中隨機抽取6個,則從
的蘋果中隨機抽取6個,則從![]() ,
,![]() 的蘋果中各抽取幾個?
的蘋果中各抽取幾個?
(Ⅱ)從(Ⅰ)中選出的6個蘋果中隨機抽取2個,求這兩個蘋果單果直徑均在![]() 內的概率;
內的概率;
(Ⅲ)以此莖葉圖中單果直徑出現的頻率代表概率,若該合作農場的果園有20萬個蘋果約5萬千克待出售,某電商提出兩種收購方案:方案![]() :所有蘋果均以5.5元/千克收購;方案
:所有蘋果均以5.5元/千克收購;方案![]() :按蘋果單果直徑大小分3類裝箱收購,每箱裝25個蘋果,定價收購方式為:單果直徑在
:按蘋果單果直徑大小分3類裝箱收購,每箱裝25個蘋果,定價收購方式為:單果直徑在![]() 內按35元/箱收購,在
內按35元/箱收購,在![]() 內按45元/箱收購,在
內按45元/箱收購,在![]() 內按55元/箱收購.包裝箱與分揀裝箱費用為5元/箱(該費用由合作農場承擔).請你通過計算為該合作農場推薦收益最好的方案.
內按55元/箱收購.包裝箱與分揀裝箱費用為5元/箱(該費用由合作農場承擔).請你通過計算為該合作農場推薦收益最好的方案.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com