
(本題滿分14分)已知函數 (
( ,實數
,實數 ,
, 為常數).
為常數).
(Ⅰ)若 ,求函數
,求函數 的極值;
的極值;
(Ⅱ)若 ,討論函數
,討論函數 的單調性.
的單調性.
解:
(Ⅰ) 在
在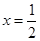 處取得極小值
處取得極小值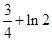 .
.
(Ⅱ)當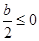 ,即
,即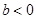 時,函數
時,函數 的單調遞減區間為
的單調遞減區間為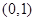 ,單調遞增區間為
,單調遞增區間為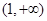 ;
;
當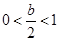 ,即
,即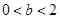 時,函數
時,函數 的單調遞增區間為
的單調遞增區間為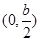 ,
,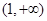 ,單調遞減區間為
,單調遞減區間為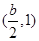 ;
;
當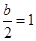 ,即
,即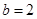 時,函數
時,函數 的單調遞增區間為
的單調遞增區間為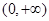 ;
;
當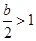 ,即
,即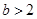 時,函數
時,函數 的單調遞增區間為
的單調遞增區間為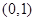 ,
,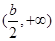 ,單調遞減區間為
,單調遞減區間為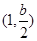 .…………………
.…………………
【解析】解:(Ⅰ)函數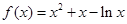 ,則
,則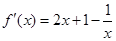 ,…………………1分
,…………………1分
令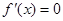 ,得
,得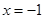 (舍去),
(舍去),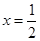 .
…………………………………………2分
.
…………………………………………2分
當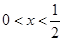 時,
時,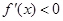 ,函數單調遞減;…………………………………………3分
,函數單調遞減;…………………………………………3分
當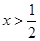 時,
時,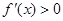 ,函數單調遞增;…………………………………………4分
,函數單調遞增;…………………………………………4分
∴ 在
在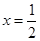 處取得極小值
處取得極小值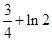 .
……………………………………5分
.
……………………………………5分
(Ⅱ)由于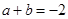 ,則
,則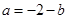 ,從而
,從而 ,則
,則
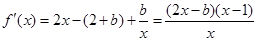 …………………………………………6分
…………………………………………6分
令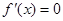 ,得
,得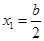 ,
, .
………………………………………7分
.
………………………………………7分
①
當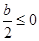 ,即
,即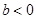 時,函數
時,函數 的單調遞減區間為
的單調遞減區間為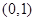 ,單調遞增區間為
,單調遞增區間為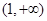 ;8分
;8分
②
當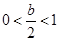 ,即
,即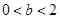 時,列表如下:
時,列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
所以,函數 的單調遞增區間為
的單調遞增區間為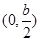 ,
,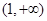 ,單調遞減區間為
,單調遞減區間為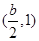 ;…………10分
;…………10分
當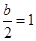 ,即
,即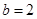 時,函數
時,函數 的單調遞增區間為
的單調遞增區間為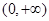 ;……………11分
;……………11分
③
當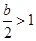 ,即
,即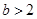 時,列表如下:
時,列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
所以函數 的單調遞增區間為
的單調遞增區間為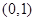 ,
,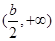 ,單調遞減區間為
,單調遞減區間為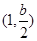 ; ……………13分
; ……………13分
綜上:當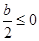 ,即
,即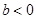 時,函數
時,函數 的單調遞減區間為
的單調遞減區間為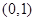 ,單調遞增區間為
,單調遞增區間為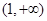 ;
;
當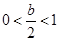 ,即
,即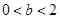 時,函數
時,函數 的單調遞增區間為
的單調遞增區間為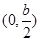 ,
,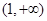 ,單調遞減區間為
,單調遞減區間為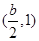 ;
;
當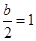 ,即
,即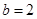 時,函數
時,函數 的單調遞增區間為
的單調遞增區間為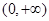 ;
;
當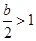 ,即
,即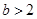 時,函數
時,函數 的單調遞增區間為
的單調遞增區間為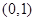 ,
,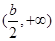 ,單調遞減區間為
,單調遞減區間為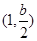 .…………………………14分
.…………………………14分


 永乾教育寒假作業快樂假期延邊人民出版社系列答案
永乾教育寒假作業快樂假期延邊人民出版社系列答案科目:高中數學 來源:2012-2013學年吉林省高三第一次月考文科數學試卷(解析版) 題型:解答題
(本題滿分14分)已知函數
(1)若 ,求x的值;
,求x的值;
(2)若 對于
對于 恒成立,求實數m的取值范圍.
恒成立,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省惠州市高三第三次調研考試數學理卷 題型:解答題
(本題滿分14分)
已知橢圓 :
: 的離心率為
的離心率為 ,過坐標原點
,過坐標原點 且斜率為
且斜率為 的直線
的直線 與
與 相交于
相交于 、
、 ,
, .
.
⑴求 、
、 的值;
的值;
⑵若動圓 與橢圓
與橢圓 和直線
和直線 都沒有公共點,試求
都沒有公共點,試求 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2010-2011學年廣東省惠州市高三第三次調研考試數學理卷 題型:解答題
((本題滿分14分)
已知梯形ABCD中,AD∥BC,∠ABC =∠BAD = ,AB=BC=2AD=4,E、F分別是AB、CD上的點,EF∥BC,AE = x,G是BC的中點.沿EF將梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如圖).
,AB=BC=2AD=4,E、F分別是AB、CD上的點,EF∥BC,AE = x,G是BC的中點.沿EF將梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如圖).
(1)當x=2時,求證:BD⊥EG ;
(2)若以F、B、C、D為頂點的三棱錐的體積記為 ,
,
求 的最大值;
的最大值;


(3)當 取得最大值時,求二面角D-BF-C的余弦值.
取得最大值時,求二面角D-BF-C的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com