【題目】謝爾賓斯基三角形（Sierpinskitriangle）是一種分形幾何圖形，由波蘭數學家謝爾賓斯基在1915年提出，它是一個自相似的例子，其構造方法是：
（1）取一個實心的等邊三角形（圖1）；
（2）沿三邊中點的連線，將它分成四個小三角形；
（3）挖去中間的那一個小三角形（圖2）；
（4）對其余三個小三角形重復（1）（2）（3）（4）（圖3）.
制作出來的圖形如圖4，圖5，….
若圖3（陰影部分）的面積為1，則圖5（陰影部分）的面積為（ ）
A.
B.
C.
D.
字詞句篇與同步作文達標系列答案科目：高中數學 來源： 題型：
【題目】某市2013年發放汽車牌照12萬張，其中燃油型汽車牌照10萬張，電動型汽車2萬張，為了節能減排和控制總量，從2013年開始，每年電動型汽車牌照按50%增長，而燃油型汽車牌照每一年比上一年減少0．5萬張，同時規定一旦某年發放的牌照超過15萬張，以后每一年發放的電動車的牌照的數量維持在這一年的水平不變．
（1）記2013年為第一年，每年發放的燃油型汽車牌照數量構成數列
，每年發放電動型汽車牌照數為構成數列
，完成下列表格，并寫出這兩個數列的通項公式；
（2）從2013年算起，累計各年發放的牌照數，哪一年開始超過200萬張？
|
|
|
| |
|
|
|
|
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，四棱錐
的底面
是直角梯形,
,
,側面
底面,
是等邊三角形，
，點
分別是棱
的中點 .
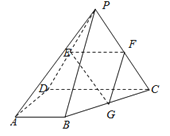
（Ⅰ）求證：
平面
；
（Ⅱ）求二面角
的大小；
（Ⅲ）在線段
上存在一點
，使
平面
，且
，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為了解學生自主學習期間完成數學套卷的情況，一名教師對某班級的所有學生進行了調查，調查結果如下表.
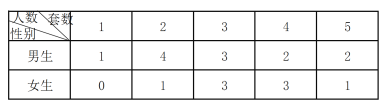
（1）從這班學生中任選一名男生，一名女生，求這兩名學生完成套卷數之和為4的概率？
（2）若從完成套卷數不少于4套的學生中任選4人，設選到的男學生人數為
，求隨機變量的分布列和數學期望；
（3）試判斷男學生完成套卷數的方差
與女學生完成套卷數的方差
的大小（只需寫出結論）.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】[選修4—4：坐標系與參數方程]
在直角坐標系
中，曲線
的方程為
．以坐標原點為極點，
軸正半軸為極軸建立極坐標系，曲線
的極坐標方程為
．
（1）求的直角坐標方程；
（2）若與有且僅有三個公共點，求的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在位于城市A南偏西
相距100海里的B處，一股臺風沿著正東方向襲來，風速為120海里/小時，臺風影響的半徑為
海里
（1）若
，求臺風影響城市A持續的時間（精確到1分鐘）？
（2）若臺風影響城市A持續的時間不超過1小時，求
的取值范圍
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
