
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,左、右焦點分別為
,左、右焦點分別為![]() 、
、![]() ,
,![]() 為相圓
為相圓![]() 上一點,
上一點,![]() 與
與![]() 軸交于
軸交于![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)過右焦點![]() 的直線
的直線![]() 交橢圓于
交橢圓于![]() 、
、![]() 兩點若
兩點若![]() 的中點為
的中點為![]() ,
,![]() 為原點,直線
為原點,直線![]() 交直線
交直線![]() 于點
于點![]() .求
.求![]() 的最大值.
的最大值.
【答案】(I)![]() ;(II)
;(II)![]()
【解析】
(Ⅰ)由題意得![]() ,通過平面幾何的知識,可以得到
,通過平面幾何的知識,可以得到![]() ,根據(jù)
,根據(jù)![]() ,離心率為
,離心率為![]() ,結合
,結合![]() ,這樣可以求出
,這樣可以求出![]() ,
,![]() ,進而求出橢圓的標準方程;
,進而求出橢圓的標準方程;
(II)直線與橢圓方程聯(lián)立,可以得到一個一元二次方程,設![]() 、
、![]() ,利用根與系數(shù)關系可以求出
,利用根與系數(shù)關系可以求出![]() 的坐標,以及
的坐標,以及![]() 的長度,求出直線
的長度,求出直線![]() 的方程,求出
的方程,求出![]() 的坐標,求出
的坐標,求出![]() 的長度表達式,求出
的長度表達式,求出 ![]() 平方的表達式,用換元法、配方法,最后求出
平方的表達式,用換元法、配方法,最后求出![]() 的最大值.
的最大值.
(I)連接![]() ,由題意得
,由題意得![]() ,所以
,所以![]() 為
為![]() 的中位線,
的中位線,
又因為![]() ,所以
,所以![]() ,且
,且![]()
又![]() ,
,![]() ,得
,得![]() ,
,![]() ,
,
故所求橢圓方程為![]() .
.
(II)聯(lián)立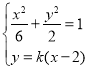 ,可得
,可得![]() .
.
設![]() 、
、![]() ,則
,則![]() ,
,![]() ,
,
所以為![]()
所以![]() 的中點
的中點![]() 坐標為
坐標為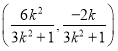 ,
,![]()
因此直線![]() 的方程為
的方程為![]() ,從而點
,從而點![]() 為
為![]() ,
,![]() ,
,
設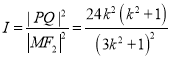 ,令
,令![]() ,則
,則
![]()
![]()
 ,
,
因此當![]() ,即
,即![]() 時
時![]() 取得最大值
取得最大值![]() .
.


科目:高中數(shù)學 來源: 題型:
【題目】如圖所示,在三棱錐P–ABC中,PA⊥平面ABC,D是棱PB的中點,已知PA=BC=2,AB=4,CB⊥AB,則異面直線PC,AD所成角的余弦值為
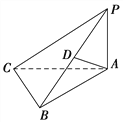
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】黨的十九大明確把精準脫貧作為決勝全面建成小康社會必須打好的三大攻堅戰(zhàn)之一,為堅決打贏脫貧攻堅戰(zhàn),某幫扶單位為幫助定點扶貧村扶貧. 此幫扶單位為了了解某地區(qū)貧困戶對其所提供的幫扶的滿意度,隨機調(diào)查了40個貧困戶,得到貧困戶的滿意度評分如下:
貧困戶編號 | 評分 | 貧困戶編號 | 評分 | 貧困戶編號 | 評分 | 貧困戶編號 | 評分 | |||
1 2 3 4 5 6 7 8 9 10 | 78 73 81 92 95 85 79 84 63 86 | 11 12 13 14 15 16 17 18 19 20 | 88 86 95 76 97 78 88 82 76 89 | 21 22 23 24 25 26 27 28 29 30 | 79 83 72 74 91 66 80 83 74 82 | 31 32 33 34 35 36 37 38 39 40 | 93 78 75 81 84 77 81 76 85 89 |
用系統(tǒng)抽樣法從40名貧困戶中抽取容量為10的樣本,且在第一分段里隨機抽到的評分數(shù)據(jù)為92.
(1)請你列出抽到的10個樣本的評分數(shù)據(jù);
(2)計算所抽到的10個樣本的均值![]() 和方差
和方差![]() ;
;
(3)在(2)條件下,若貧困戶的滿意度評分在![]() 之間,則滿意度等級為“
之間,則滿意度等級為“![]() 級”.運用樣本估計總體的思想,現(xiàn)從(1)中抽到的10個樣本的滿意度為“
級”.運用樣本估計總體的思想,現(xiàn)從(1)中抽到的10個樣本的滿意度為“![]() 級”貧困戶中隨機地抽取2戶,求所抽到2戶的滿意度均評分均“超過80”的概率.
級”貧困戶中隨機地抽取2戶,求所抽到2戶的滿意度均評分均“超過80”的概率.
(參考數(shù)據(jù):![]() )
)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某文體局為了解“跑團”每月跑步的平均里程,收集并整理了2018年1月至2018年11月期間“跑團”每月跑步的平均里程(單位:公里)的數(shù)據(jù),繪制了下面的折線圖.根據(jù)折線圖,下列結論正確的是( )

A. 月跑步平均里程的中位數(shù)為6月份對應的里程數(shù)
B. 月跑步平均里程逐月增加
C. 月跑步平均里程高峰期大致在8、9月
D. 1月至5月的月跑步平均里程相對于6月至11月,波動性更小,變化比較平穩(wěn)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知過原點的動直線![]() 與圓
與圓![]() :
:![]() 相交于不同的兩點
相交于不同的兩點![]() ,
,![]() .
.
(1)求圓![]() 的圓心坐標;
的圓心坐標;
(2)求線段![]() 的中點
的中點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(3)是否存在實數(shù)![]() ,使得直線
,使得直線![]() :
:![]() 與曲線
與曲線![]() 只有一個交點?若存在,求出
只有一個交點?若存在,求出![]() 的取值范圍;若不存在,說明理由.
的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
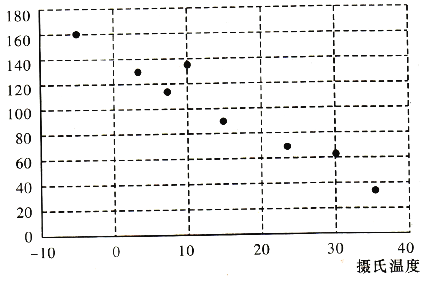
【題目】有一個同學家開了一個小賣部,他為了研究氣溫對熱飲飲料銷售的影響,經(jīng)過統(tǒng)計,得到一個賣出的熱飲杯數(shù)與當天氣溫的散點圖和對比表:
攝氏溫度 |
|
|
|
|
|
|
|
|
熱飲杯數(shù) |
|
|
|
|
|
|
|
|
(1)從散點圖可以發(fā)現(xiàn),各點散布在從左上角到右下角的區(qū)域里。因此,氣溫與當天熱飲銷售杯數(shù)之間成負相關,即氣溫越高,當天賣出去的熱飲杯數(shù)越少。統(tǒng)計中常用相關系數(shù)![]() 來衡量兩個變量之間線性關系的強弱.統(tǒng)計學認為,對于變量
來衡量兩個變量之間線性關系的強弱.統(tǒng)計學認為,對于變量![]() 、
、![]() ,如果
,如果![]() ,那么負相關很強;如果
,那么負相關很強;如果![]() ,那么正相關很強;如果
,那么正相關很強;如果![]() ,那么相關性一般;如果
,那么相關性一般;如果![]() ,那么相關性較弱。請根據(jù)已知數(shù)據(jù),判斷氣溫與當天熱飲銷售杯數(shù)相關性的強弱.
,那么相關性較弱。請根據(jù)已知數(shù)據(jù),判斷氣溫與當天熱飲銷售杯數(shù)相關性的強弱.
(2)(i)請根據(jù)已知數(shù)據(jù)求出氣溫與當天熱飲銷售杯數(shù)的線性回歸方程;
(ii)記![]() 為不超過
為不超過![]() 的最大整數(shù),如
的最大整數(shù),如![]() ,
,![]() .對于(i)中求出的線性回歸方程
.對于(i)中求出的線性回歸方程![]() ,將
,將![]() 視為氣溫與當天熱飲銷售杯數(shù)的函數(shù)關系.已知氣溫
視為氣溫與當天熱飲銷售杯數(shù)的函數(shù)關系.已知氣溫![]() 與當天熱飲每杯的銷售利潤
與當天熱飲每杯的銷售利潤![]() 的關系是
的關系是![]()
![]() (單位:元),請問當氣溫
(單位:元),請問當氣溫![]() 為多少時,當天的熱飲銷售利潤總額最大?
為多少時,當天的熱飲銷售利潤總額最大?
(參考公式)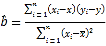 ,
,![]() ,
,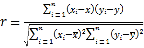
(參考數(shù)據(jù))![]() ,
,![]() ,
,![]()
![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某社區(qū)消費者協(xié)會為了解本社區(qū)居民網(wǎng)購消費情況,隨機抽取了100位居民作為樣本,就最近一年來網(wǎng)購消費金額(單位:千元),網(wǎng)購次數(shù)和支付方式等進行了問卷調(diào)査.經(jīng)統(tǒng)計這100位居民的網(wǎng)購消費金額均在區(qū)間![]() 內(nèi),按
內(nèi),按![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分成6組,其頻率分布直方圖如圖所示.
分成6組,其頻率分布直方圖如圖所示.
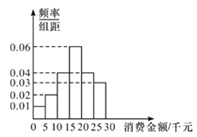
(1)估計該社區(qū)居民最近一年來網(wǎng)購消費金額的中位數(shù);
(2)將網(wǎng)購消費金額在20千元以上者稱為“網(wǎng)購迷”,補全下面的![]() 列聯(lián)表,并判斷有多大把握認為“網(wǎng)購迷與性別有關系”;
列聯(lián)表,并判斷有多大把握認為“網(wǎng)購迷與性別有關系”;
男 | 女 | 合計 | |
網(wǎng)購迷 | 20 | ||
非網(wǎng)購迷 | 45 | ||
合計 | 100 |
(3)調(diào)査顯示,甲、乙兩人每次網(wǎng)購采用的支付方式相互獨立,兩人網(wǎng)購時間與次數(shù)也互不. 影響.統(tǒng)計最近一年來兩人網(wǎng)購的總次數(shù)與支付方式,所得數(shù)據(jù)如下表所示:
網(wǎng)購總次數(shù) | 支付寶支付次數(shù) | 銀行卡支付次數(shù) | 微信支付次數(shù) | |
甲 | 80 | 40 | 16 | 24 |
乙 | 90 | 60 | 18 | 12 |
將頻率視為概率,若甲、乙兩人在下周內(nèi)各自網(wǎng)購2次,記兩人采用支付寶支付的次數(shù)之和為![]() ,求
,求![]() 的數(shù)學期望.
的數(shù)學期望.
附:觀測值公式: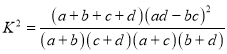
臨界值表:
| 0.01 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知三棱錐P-ABC(如圖1)的展開圖如圖2,其中四邊形ABCD為邊長等于![]() 的正方形,△ABE和△BCF均為正三角形,在三棱錐P-ABC中.
的正方形,△ABE和△BCF均為正三角形,在三棱錐P-ABC中.
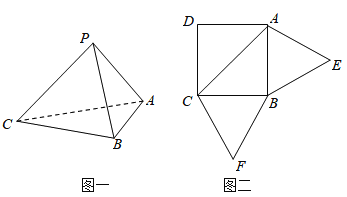
(1)證明:平面PAC⊥平面ABC;
(2)若M,N分別是AP,BC的中點,請判斷三棱錐M-BCP和三棱錐N-APC體積的大小關系并加以證明.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】為迎接2022年冬奧會,北京市組織中學生開展冰雪運動的培訓活動,并在培訓結束后對學生進行了考核.記![]() 表示學生的考核成績,并規(guī)定
表示學生的考核成績,并規(guī)定![]() 為考核優(yōu)秀.為了了解本次培訓活動的效果,在參加培訓的學生中隨機抽取了30名學生的考核成績,并作成如下莖葉圖:
為考核優(yōu)秀.為了了解本次培訓活動的效果,在參加培訓的學生中隨機抽取了30名學生的考核成績,并作成如下莖葉圖:

(Ⅰ)從參加培訓的學生中隨機選取1人,請根據(jù)圖中數(shù)據(jù),估計這名學生考核優(yōu)秀的概率;
(Ⅱ)從圖中考核成績滿足![]() 的學生中任取2人,求至少有一人考核優(yōu)秀的概率;
的學生中任取2人,求至少有一人考核優(yōu)秀的概率;
(Ⅲ)記![]() 表示學生的考核成績在區(qū)間
表示學生的考核成績在區(qū)間![]() 的概率,根據(jù)以往培訓數(shù)據(jù),規(guī)定當
的概率,根據(jù)以往培訓數(shù)據(jù),規(guī)定當![]() 時培訓有效.請根據(jù)圖中數(shù)據(jù),判斷此次中學生冰雪培訓活動是否有效,并說明理由.
時培訓有效.請根據(jù)圖中數(shù)據(jù),判斷此次中學生冰雪培訓活動是否有效,并說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com