【題目】（本小題滿分12分）
在
中，內角
對邊的邊長分別是
，已知
，
．
（Ⅰ）若
的面積等于
，求
；
（Ⅱ）若
，求
的面積．
【答案】（Ⅰ）
，
，（Ⅱ）
【解析】
（Ⅰ）由余弦定理及已知條件得，
，
又因為
的面積等于
，所以
，得
．··········································4分
聯立方程組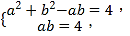
解得，．··················································6分
（Ⅱ）由題意得
，
即
，······························································8分
當
時，
，
，
，
，
當
時，得
，由正弦定理得
，
聯立方程組
解得
，
．
所以
的面積
．······················································12分
科目：高中數學 來源： 題型：
【題目】已知函數f（x）= 
﹣ 
﹣ax（a∈R）．
（1）當a= 
時，求函數f（x）的單調區間；
（2）若函數f（x）在[﹣1，1]上為單調函數，求實數a的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列{an}（n∈N*）是公差不為0的等差數列，a1=1，且 
， 
， 
成等比數列．
（1）求數列{an}的通項公式；
（2）設數列{ 
}的前n項和為Tn ， 求證：Tn＜1．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設a，b是正奇數，數列{cn}（n∈N*）定義如下：c1=a，c2=b，對任意n≥3，cn是cn﹣1+cn﹣2的最大奇約數．數列{cn}中的所有項構成集合A．
（1）若a=9，b=15，寫出集合A；
（2）對k≥1，令dk=max{c2k ， c2k﹣1}（max{p，q}表示p，q中的較大值），求證：dk+1≤dk；
（3）證明集合A是有限集，并寫出集合A中的最小數．】
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知△ABC內角A，B，C的對邊分別是a，b，c，且滿足a（ 
sinC+cosC）=b+c．
（I） 求角A的大小；
（Ⅱ）已知函數f（x）=sin（ωx+A）的最小正周期為π，求f（x）的減區間．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=xlnx﹣ax2+ 
．
（I） 當a= 時，判斷f（x）在其定義上的單調性；
（Ⅱ）若函數f（x）有兩個極值點x1 ， x2 ， 其中x1＜x2 ． 求證：
（i）f（x2）＞0；
（ii）x1+x2＞ 
．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】（本題滿分15分）如圖，在四棱錐
中，平面PAD⊥平面ABCD， 
，
，E是BD的中點．
（Ⅰ）求證：EC//平面APD；
（Ⅱ）求BP與平面ABCD所成角的正切值；
（Ⅲ）求二面角
的正弦值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
