
【題目】已知橢圓C: ![]() =1(a>b>0)的離心率為
=1(a>b>0)的離心率為 ![]() ,以原點為圓心,橢圓的短半軸為半徑的圓與直線x﹣y+
,以原點為圓心,橢圓的短半軸為半徑的圓與直線x﹣y+ ![]() =0相切,過點P(4,0)且不垂直于x軸直線l與橢圓C相交于A、B兩點.
=0相切,過點P(4,0)且不垂直于x軸直線l與橢圓C相交于A、B兩點.
(1)求橢圓C的方程;
(2)求 ![]() 的取值范圍;
的取值范圍;
(3)若B點關(guān)于x軸的對稱點是E,證明:直線AE與x軸相交于定點.
【答案】
(1)解:由題意知, ![]() ,
, ![]() 即b=
即b= ![]()
又a2=b2+c2
∴a=2,b= ![]()
故橢圓的方程為 ![]()
(2)解:由題意知直線l的斜率存在,設(shè)直線l的方程為y=k(x﹣4)
由 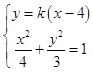 可得:(3+4k2)x2﹣32k2x+64k2﹣12=0
可得:(3+4k2)x2﹣32k2x+64k2﹣12=0
設(shè)A(x1,y1),B (x2,y2),則△=322k4﹣4(3+4k2)(64k2﹣12)>0
∴ ![]()
∴x1+x2= ![]() ,x1x2=
,x1x2= ![]() ①
①
∴ ![]() =x1x2+y1y2=
=x1x2+y1y2= ![]()
= ![]()
= ![]()
= ![]()
∵ ![]()
∴ ![]()
∴ ![]()
∴ ![]()
![]()
(3)證明:∵B,E關(guān)于x軸對稱
∴可設(shè)E(x2,﹣y2)
∴直線AE的方程為 ![]()
令y=0可得x= ![]()
∵y1=k(x1﹣4),y2=k(x2﹣4)
∴ ![]() =
= 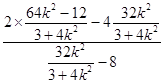 =1
=1
∴直線AE與x軸交于定點(1,0)
【解析】(1)由題意知, ![]() ,利用點到直線的距離公式可求b,結(jié)合a2=b2+c2可求a,即可求解(2)由題意設(shè)直線l的方程為y=k(x﹣4),聯(lián)立直線與橢圓方程,設(shè)A(x1 , y1),B (x2 , y2),根據(jù)方程的根與系數(shù)關(guān)系求出x1+x2 , x1x2 , 由△>0可求k的范圍,然后代入
,利用點到直線的距離公式可求b,結(jié)合a2=b2+c2可求a,即可求解(2)由題意設(shè)直線l的方程為y=k(x﹣4),聯(lián)立直線與橢圓方程,設(shè)A(x1 , y1),B (x2 , y2),根據(jù)方程的根與系數(shù)關(guān)系求出x1+x2 , x1x2 , 由△>0可求k的范圍,然后代入 ![]() =x1x2+y1y2=
=x1x2+y1y2= ![]() =
= ![]() 中即可得關(guān)于k的方程,結(jié)合k的范圍可求
中即可得關(guān)于k的方程,結(jié)合k的范圍可求 ![]() 的范圍(3)由B,E關(guān)于x軸對稱可得E(x2 , ﹣y2),寫出AE的方程,令y=0,結(jié)合(2)可求
的范圍(3)由B,E關(guān)于x軸對稱可得E(x2 , ﹣y2),寫出AE的方程,令y=0,結(jié)合(2)可求
【考點精析】解答此題的關(guān)鍵在于理解橢圓的標準方程的相關(guān)知識,掌握橢圓標準方程焦點在x軸:![]() ,焦點在y軸:
,焦點在y軸:![]() .
.


科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,AC1是正方體ABCD﹣A1B1C1D1的對角線. 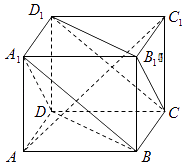
(1)求證:平面A1BD∥平面CD1B1;
(2)求證:直線AC1⊥直線BD.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】關(guān)于平面向量,有下列四個命題:
①若 ![]() .
.
② ![]() =(1,1),
=(1,1), ![]() =(2,x),若
=(2,x),若 ![]() 與
與 ![]() 平行,則x=2.
平行,則x=2.
③非零向量 ![]() 和
和 ![]() 滿足|
滿足| ![]() |=|
|=| ![]() |=|
|=| ![]() |,則
|,則 ![]() 與
與 ![]() 的夾角為60°.
的夾角為60°.
④點A(1,3),B(4,﹣1),與向量 ![]() 同方向的單位向量為(
同方向的單位向量為( ![]() ).
).
其中真命題的序號為 . (寫出所有真命題的序號)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某小學(xué)對五年級的學(xué)生進行體質(zhì)測試,已知五年一班共有學(xué)生30人,測試立定跳遠的成績用莖葉圖表示如圖(單位:cm): 男生成績在175cm以上(包括175cm)定義為“合格”,成績在175cm以下(不包括175cm)定義為“不合格”.
女生成績在165cm以上(包括165cm)定義為“合格”,成績在165cm以下(不包括165cm)定義為“不合格”.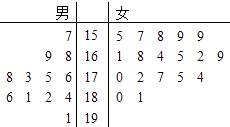
(1)求五年一班的女生立定跳遠成績的中位數(shù);
(2)在五年一班的男生中任意選取3人,求至少有2人的成績是合格的概率;
(3)若從五年一班成績“合格”的學(xué)生中選取2人參加復(fù)試,用X表示其中男生的人數(shù),寫出X的分布列,并求X的數(shù)學(xué)期望.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某校從高一年級A,B兩個班中各選出7名學(xué)生參加物理競賽,他們的成績(單位:分)的莖葉圖如圖所示,其中A班學(xué)生的平均分是85分 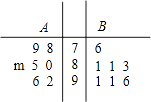
(1)求m的值,并計算A班7名學(xué)生成績的方差s2;
(2)從成績在90分以上的學(xué)生中隨機抽取兩名學(xué)生,求至少有一名A班學(xué)生的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() (
(![]() 是自然對數(shù)的底數(shù)).
是自然對數(shù)的底數(shù)).
(1)若![]() ,求函數(shù)
,求函數(shù)![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若![]() 在
在![]() 內(nèi)無極值,求
內(nèi)無極值,求![]() 的取值范圍;
的取值范圍;
(3)設(shè)![]() ,求證:
,求證: ![]() 。
。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標系xOy中,已知向量 ![]() =(
=( ![]() ,﹣
,﹣ ![]() ),
), ![]() =(sinx,cosx),x∈(0,
=(sinx,cosx),x∈(0, ![]() ).
).
(1)若 ![]() ⊥
⊥ ![]() ,求tanx的值;
,求tanx的值;
(2)若 ![]() 與
與 ![]() 的夾角為
的夾角為 ![]() ,求x的值.
,求x的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知a>0,b>0,且a2+b2= ![]() ,若a+b≤m恒成立, (Ⅰ)求m的最小值;
,若a+b≤m恒成立, (Ⅰ)求m的最小值;
(Ⅱ)若2|x﹣1|+|x|≥a+b對任意的a,b恒成立,求實數(shù)x的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com