
【題目】如圖,已知四棱錐![]() 的底面是等腰梯形,
的底面是等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 為等邊三角形,且點P在底面
為等邊三角形,且點P在底面![]() 上的射影為
上的射影為![]() 的中點G,點E在線段
的中點G,點E在線段![]() 上,且
上,且![]() .
.
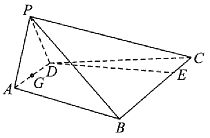
(1)求證:![]() 平面
平面![]() .
.
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)證明見解析(2)![]()
【解析】
(1)由等腰梯形的性質可證得![]() ,由射影可得
,由射影可得![]() 平面
平面![]() ,進而求證;
,進而求證;
(2)取![]() 的中點F,連接
的中點F,連接![]() ,以G為原點,
,以G為原點,![]() 所在直線為x軸,
所在直線為x軸,![]() 所在直線為y軸,
所在直線為y軸,![]() 所在直線為z軸,建立空間直角坐標系,分別求得平面
所在直線為z軸,建立空間直角坐標系,分別求得平面![]() 與平面
與平面![]() 的法向量,再利用數量積求解即可.
的法向量,再利用數量積求解即可.
(1)在等腰梯形![]() 中,
中,
![]() 點E在線段
點E在線段![]() 上,且
上,且![]() ,
,
![]() 點E為
點E為![]() 上靠近C點的四等分點,
上靠近C點的四等分點,
![]()
![]() ,
,![]() ,
,![]() ,
,
![]()
![]() ,
,
![]() 點P在底面
點P在底面![]() 上的射影為
上的射影為![]() 的中點G,連接
的中點G,連接![]() ,
,
![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() .
.
又![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() .
.
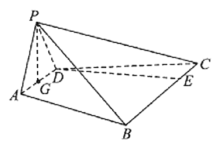
(2)取![]() 的中點F,連接
的中點F,連接![]() ,以G為原點,
,以G為原點,![]() 所在直線為x軸,
所在直線為x軸,![]() 所在直線為y軸,
所在直線為y軸,![]() 所在直線為z軸,建立空間直角坐標系,如圖所示,
所在直線為z軸,建立空間直角坐標系,如圖所示,
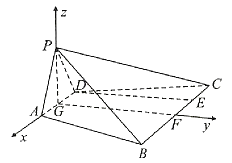
由(1)易知,![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
![]() ,
,![]() 為等邊三角形,
為等邊三角形,![]() ,
,
則![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,
,
則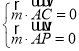 ,即
,即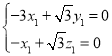 ,
,
令![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,
設平面![]() 的法向量為
的法向量為![]() ,
,
則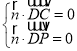 ,即
,即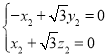 ,
,
令![]() ,則
,則![]() ,
,![]() ,
,![]() ,
,
設平面![]() 與平面
與平面![]() 的夾角為θ,則
的夾角為θ,則
![]()
![]() 二面角
二面角![]() 的余弦值為
的余弦值為![]() .
.


 津橋教育計算小狀元系列答案
津橋教育計算小狀元系列答案科目:高中數學 來源: 題型:
【題目】一對夫婦為了給他們的獨生孩子支付將來上大學的費用,從孩子一周歲生日開始,每年到銀行儲蓄![]() 元一年定期,若年利率為
元一年定期,若年利率為![]() 保持不變,且每年到期時存款(含利息)自動轉為新的一年定期,當孩子18歲生日時不再存入,將所有存款(含利息)全部取回,則取回的錢的總數為
保持不變,且每年到期時存款(含利息)自動轉為新的一年定期,當孩子18歲生日時不再存入,將所有存款(含利息)全部取回,則取回的錢的總數為![]()
![]()
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】流行性感冒(簡稱流感)是流感病毒引起的急性呼吸道感染,是一種傳染性強、傳播速度快的疾病.其主要通過空氣中的飛沫、人與人之間的接觸或與被污染物品的接觸傳播.流感每年在世界各地均有傳播,在我國北方通常呈冬春季流行,南方有冬春季和夏季兩個流行高峰.兒童相對免疫力低,在幼兒園、學校等人員密集的地方更容易被傳染.某幼兒園將去年春期該園患流感小朋友按照年齡與人數統計,得到如下數據:
年齡( |
|
|
|
|
|
患病人數( |
|
|
|
|
|
(1)求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(2)計算變量![]() 、
、![]() 的相關系數
的相關系數![]() (計算結果精確到
(計算結果精確到![]() ),并回答是否可以認為該幼兒園去年春期患流感人數與年齡負相關很強?(若
),并回答是否可以認為該幼兒園去年春期患流感人數與年齡負相關很強?(若![]() ,則
,則![]() 、
、![]() 相關性很強;若
相關性很強;若![]() ,則
,則![]() 、
、![]() 相關性一般;若
相關性一般;若![]() ,則
,則![]() 、
、![]() 相關性較弱.)
相關性較弱.)
參考數據:![]() .
.
參考公式: ,
,
相關系數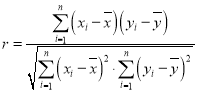 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“中國剩余定理”又稱“孫子定理”,最早可見于中國南北朝時期的數學著作《孫子算經》卷下第二十六題,叫做“物不知數”,原文如下:今有物不知其數,三三數之剩二,五五數之剩三,七七數之剩二.問物幾何?現有這樣一個相關的問題:將1到2020這2020個自然數中被5除余3且被7除余2的數按照從小到大的順序排成一列,構成一個數列,則該數列各項之和為( )
A.56383B.57171C.59189D.61242
查看答案和解析>>
科目:高中數學 來源: 題型:
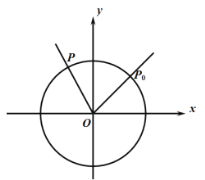
【題目】如圖,單位圓上有一點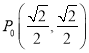 ,點
,點![]() 以點
以點![]() 為起點按逆時針方向以每秒
為起點按逆時針方向以每秒![]() 弧度作圓周運動,點
弧度作圓周運動,點![]() 的縱坐標
的縱坐標![]() 是關于時間
是關于時間![]() 的函數,記作
的函數,記作![]() .
.
(1)當![]() 時,求
時,求![]() ;
;
(2)若將函數![]() 向左平移
向左平移![]() 個單位長度后,得到的曲線關于
個單位長度后,得到的曲線關于![]() 軸對稱,求
軸對稱,求![]() 的最小正值,并求此時
的最小正值,并求此時![]() 在
在![]() 的值域.
的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠連續6天對新研發的產品按事先擬定的價格進行試銷,得到一組數據![]() 如下表所示
如下表所示
日期 | 4月1日 | 4月2日 | 4月3日 | 4月4日 | 4月5日 | 4月6日 |
試銷價 | 9 | 11 | 10 | 12 | 13 | 14 |
產品銷量 | 40 | 32 | 29 | 35 | 44 |
|
(1)試根據4月2日、3日、4日的三組數據,求![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ,并預測4月6日的產品銷售量
,并預測4月6日的產品銷售量![]() ;
;
(2)若選取兩組數據確定回歸方程,求選取得兩組數據恰好是不相鄰兩天的事件![]() 的概率.
的概率.
參考公式:![]()
其中
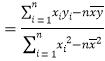 ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為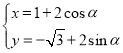 (其中
(其中![]() 為參數,
為參數,![]() ).在極坐標系(以坐標原點
).在極坐標系(以坐標原點![]() 為極點,以
為極點,以![]() 軸非負半軸為極軸)中,曲線
軸非負半軸為極軸)中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若曲線![]() 上恰有一個點到曲線
上恰有一個點到曲線![]() 的距離為1,求曲線
的距離為1,求曲線![]() 的直角坐標方程.
的直角坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設中心在原點,焦點在![]() 軸上的橢圓
軸上的橢圓![]() 過點
過點![]() ,且離心率為
,且離心率為![]() .
.![]() 為
為![]() 的右焦點,
的右焦點,![]() 為
為![]() 上一點,
上一點,![]() 軸,
軸,![]() 的半徑為
的半徑為![]() .
.
(1)求![]() 和
和![]() 的方程;
的方程;
(2)若直線![]() 與
與![]() 交于
交于![]() 兩點,與
兩點,與![]() 交于
交于![]() 兩點,其中
兩點,其中![]() 在第一象限,是否存在
在第一象限,是否存在![]() 使
使![]() ?若存在,求
?若存在,求![]() 的方程;若不存在,說明理由.
的方程;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com