Question

【題目】已知數列{an}的前n項和為Sn（n∈N*），且滿足an+2Sn=2n+2．
（1）求數列{an}的通項公式；
（2）求證： ．

Answer 1

【答案】
（1）解：∵an+2Sn=2n+2，令n=1，得 ．

由an+2Sn=2n+2得 n≥2時，an﹣1+2Sn﹣1=2（n﹣1）+2，

兩式相減得；3an=an﹣1+2，

∴ ，

∴數列{an﹣1}是以首項為 ，公比為 的等比數列，

∴ ，∴ ．

（2）證明：

∵ = ，

∴

= = =

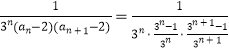【解析】（1）由an+2Sn=2n+2，利用遞推關系可得：3an=an﹣1+2，變形為 ，再利用等比數列的通項公式即可得出．（2）利用“裂項求和”方法與數列的單調性即可得出．
【考點精析】本題主要考查了數列的通項公式的相關知識點，需要掌握如果數列an的第n項與n之間的關系可以用一個公式表示，那么這個公式就叫這個數列的通項公式才能正確解答此題．