
【題目】記無窮數列![]() 的前
的前![]() 項中最大值為
項中最大值為![]() ,最小值為
,最小值為![]() ,令
,令![]() ,則稱
,則稱![]() 是
是![]() “極差數列”.
“極差數列”.
(1)若![]() ,求
,求![]() 的前
的前![]() 項和;
項和;
(2)證明:![]() 的“極差數列”仍是
的“極差數列”仍是![]() ;
;
(3)求證:若數列![]() 是等差數列,則數列
是等差數列,則數列![]() 也是等差數列.
也是等差數列.
【答案】(1)![]() (2)證明見解析(3)證明見解析
(2)證明見解析(3)證明見解析
【解析】
(1)由![]() 是遞增數列,得
是遞增數列,得![]() ,由此能求出
,由此能求出![]() 的前
的前![]() 項和.
項和.
(2)推導出![]() ,
,![]() ,由此能證明
,由此能證明![]() 的“極差數列”仍是
的“極差數列”仍是![]() .
.
(3)證當數列![]() 是等差數列時,設其公差為
是等差數列時,設其公差為![]() ,
,![]()
![]() ,
,![]() 是一個單調遞增數列,從而
是一個單調遞增數列,從而![]() ,
,![]() ,由
,由![]() ,
,![]() ,
,![]() ,分類討論,能證明若數列
,分類討論,能證明若數列![]() 是等差數列,則數列
是等差數列,則數列![]() 也是等差數列.
也是等差數列.
(1)解:∵無窮數列![]() 的前
的前![]() 項中最大值為
項中最大值為![]() ,最小值為
,最小值為![]() ,
,![]() ,
,![]() ,
,
![]() 是遞增數列,∴
是遞增數列,∴![]() ,
,
∴![]() 的前
的前![]() 項和
項和![]() .
.
(2)證明:∵![]() ,
,
![]() ,
,
∴![]()
![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() 的“極差數列”仍是
的“極差數列”仍是![]()
(3)證明:當數列![]() 是等差數列時,設其公差為
是等差數列時,設其公差為![]() ,
,
![]()
![]() ,
,
根據![]() ,
,![]() 的定義,得:
的定義,得:
![]() ,
,![]() ,且兩個不等式中至少有一個取等號,
,且兩個不等式中至少有一個取等號,
當![]() 時,必有
時,必有![]() ,∴
,∴![]() ,
,
∴![]() 是一個單調遞增數列,∴
是一個單調遞增數列,∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,∴
,∴![]() 是等差數列,
是等差數列,
當![]() 時,則必有
時,則必有![]() ,∴
,∴![]() ,
,
∴![]() 是一個單調遞減數列,∴
是一個單調遞減數列,∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .∴
.∴![]() 是等差數列,
是等差數列,
當![]() 時,
時,![]()
![]() ,
,
∵![]() ,
,![]() 中必有一個為0,
中必有一個為0,
根據上式,一個為0,為一個必為0,
∴![]() ,
,![]() ,
,
∴數列![]() 是常數數列,則數列
是常數數列,則數列![]() 是等差數列.
是等差數列.
綜上,若數列![]() 是等差數列,則數列
是等差數列,則數列![]() 也是等差數列.
也是等差數列.


科目:高中數學 來源: 題型:
【題目】某中學2018年的高考考生人數是2015年高考考生人數的![]() 倍,為了更好地對比該校考生的升學情況,統計了該校2015年和2018年的高考情況,得到如圖柱狀圖:
倍,為了更好地對比該校考生的升學情況,統計了該校2015年和2018年的高考情況,得到如圖柱狀圖:

則下列結論正確的是![]()
![]()
A. 與2015年相比,2018年一本達線人數減少
B. 與2015年相比,2018年二本達線人數增加了![]() 倍
倍
C. 2015年與2018年藝體達線人數相同
D. 與2015年相比,2018年不上線的人數有所增加
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四邊形ABCD為平行四邊形,點E在AB上,AE=2EB=2,且DE⊥AB.以DE為折痕把△ADE折起,使點A到達點F的位置,且∠FEB=60°.
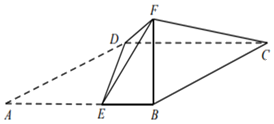
(1)求證:平面BFC⊥平面BCDE;
(2)若直線DF與平面BCDE所成角的正切值為![]() ,求二面角E﹣DF﹣C的正弦值.
,求二面角E﹣DF﹣C的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知四棱錐![]() 的正視圖是一個底邊長為4腰長為3的等腰三角形,圖1、圖2分別是四棱錐
的正視圖是一個底邊長為4腰長為3的等腰三角形,圖1、圖2分別是四棱錐![]() 的側視圖和俯視圖.
的側視圖和俯視圖.
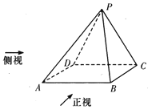
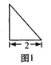
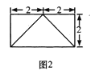
(1)求證:![]() ;
;
(2)求四棱錐![]() 的體積及側面積.
的體積及側面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了調查某大學學生的某天上網的時間,隨機對![]() 名男生和
名男生和![]() 名女生進行了不記名的問卷調查.得到了如下的統計結果:
名女生進行了不記名的問卷調查.得到了如下的統計結果:
表1:男生上網時間與頻數分布表
上網時間(分鐘) |
|
|
|
|
|
人數 |
|
|
|
|
|
表2:女生上網時間與頻數分布表
上網時間(分鐘) |
|
|
|
|
|
人數 |
|
|
|
|
|
(1)用分層抽樣在![]() 選取
選取![]() 人,再隨機抽取
人,再隨機抽取![]() 人,求抽取的
人,求抽取的![]() 人都是女生的概率;
人都是女生的概率;
(2)完成下面的![]() 列聯表,并回答能否有
列聯表,并回答能否有![]() 的把握認為“大學生上網時間與性別有關”?
的把握認為“大學生上網時間與性別有關”?
上網時間少于 | 上網時間不少于 | 合計 | |
男生 | |||
女生 | |||
合計 |
附: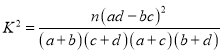
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系xOy中,直線l的參數方程為![]() ,(t為參數),在以坐標原點為極點,x軸正半軸為極軸的極坐標系中,曲線C1:ρ=2cosθ,
,(t為參數),在以坐標原點為極點,x軸正半軸為極軸的極坐標系中,曲線C1:ρ=2cosθ,![]() .
.
(1)求C1與C2交點的直角坐標;
(2)若直線l與曲線C1,C2分別相交于異于原點的點M,N,求|MN|的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】今有6個人組成的旅游團,包括4個大人,2個小孩,去廬山旅游,準備同時乘纜車觀光,現有三輛不同的纜車可供選擇,每輛纜車最多可乘3人,為了安全起見,小孩乘纜車必須要大人陪同,則不同的乘車方式有_____種.(用數字作答)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com