
 中,
中, 為矩形,平面
為矩形,平面 平面
平面 .
.

 問
問 為何值時,四棱錐
為何值時,四棱錐 的體積最大?并求此時平面
的體積最大?并求此時平面 與平面
與平面 夾角的余弦值.
夾角的余弦值. 時,四棱錐的體積P-ABCD最大. 平面BPC與平面DPC夾角的余弦值為
時,四棱錐的體積P-ABCD最大. 平面BPC與平面DPC夾角的余弦值為
 AD,又平面PAD
AD,又平面PAD 平面ABCD,平面PAD
平面ABCD,平面PAD 平面ABCD=AD,所以AB
平面ABCD=AD,所以AB 平面PAD,再根據線面垂直證線線垂直:因為PD
平面PAD,再根據線面垂直證線線垂直:因為PD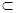 平面PAD,所以AB
平面PAD,所以AB PD
PD 平面ABCD,平面PAD
平面ABCD,平面PAD 平面ABCD=AD,所以PO
平面ABCD=AD,所以PO 平面ABCD,下面用
平面ABCD,下面用 表示高及底面積:設
表示高及底面積:設 ,則
,則 ,故四棱錐P-ABCD的體積為
,故四棱錐P-ABCD的體積為 故當
故當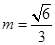 時,即
時,即 時,四棱錐的體積P-ABCD最大.
時,四棱錐的體積P-ABCD最大. AD,
AD, 平面ABCD
平面ABCD 平面ABCD=AD
平面ABCD=AD 平面PAD,因為PD
平面PAD,因為PD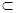 平面PAD,故AB
平面PAD,故AB PD
PD 平面ABCD,BC
平面ABCD,BC 平面POG,BC
平面POG,BC PG
PG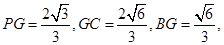
 ,則
,則 ,故四棱錐P-ABCD的體積為
,故四棱錐P-ABCD的體積為
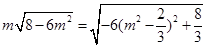
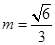 時,即
時,即 時,四棱錐的體積P-ABCD最大.
時,四棱錐的體積P-ABCD最大.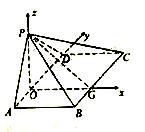

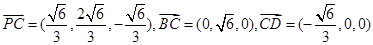
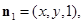 ,則由
,則由 ,
, 得
得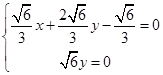


 ,從而平面BPC與平面DPC夾角
,從而平面BPC與平面DPC夾角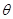 的余弦值為
的余弦值為


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:高中數學 來源:不詳 題型:解答題
 CD=1,PD=
CD=1,PD= .
.
 ?
?查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題
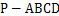 的底面
的底面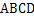 是平行四邊形,
是平行四邊形,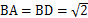 ,
,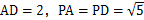 ,
,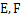 分別是棱
分別是棱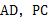 的中點.
的中點.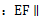 平面
平面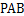 ;
;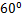 ,
,
查看答案和解析>>
科目:高中數學 來源:不詳 題型:解答題

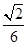 ,求線段AM的長.
,求線段AM的長.
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com