【題目】已知函數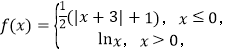
若存在實數
，滿足
，則
的最大值是____．
【答案】
.
【解析】分析: 根據函數f（x）圖象判斷a，b，c關系即范圍，用c表示出af（a）+bf（b）+cf（c），根據函數單調性求出最大值．
詳解: 作出f（x）的函數圖象如圖所示：
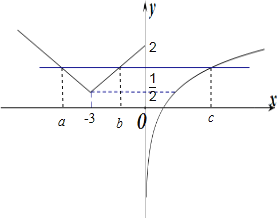
∵存在實數a＜b＜c，滿足f（a）=f（b）=f（c），
∴a+b=﹣6，
∴af（a）+bf（b）+cf（c）=（a+b+c）f（c）=（c﹣6）lnc，
由函數圖象可知：
＜c＜e2，
設g（c）=（c﹣6）lnc，則
=lnc+1﹣
，
顯然在（，e2]上單調遞增，
∵
=2﹣
＜0，
=3﹣
＞0，
∴在（，e2]上存在唯一一個零點，不妨設為c0，
在g（c）在（，c0）上單調遞減，在（c0，e2]上單調遞增，
又g（）=
（﹣6）＜0，g（e2）=2（e2﹣6）＞0，
∴g（c）的最大值為g（e2）=2e2﹣12．
故答案為：2e2﹣12
點睛: （1）本題有三個關鍵點,其一是能夠很熟練準確地畫出函數的圖像；其二是從圖像里能發現a+b=-6, ＜c＜e2；其三是能夠想到構造函數g（c）=（c﹣6）lnc，利用導數求函數的最大值.（2）本題要求函數的圖像和性質掌握的比較好，屬于中檔題.
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】在全球關注的抗擊“新冠肺炎”中，某跨國科研中心的一個團隊，研制了甲、乙兩種治療“新冠肺炎”新藥，希望知道哪種新藥更有效，為此進行動物試驗，試驗方案如下：
第一種：選取
共10只患病白鼠，服用甲藥后某項指標分別為：
；
第二種：選取
共10只患病白鼠，服用乙藥后某項指標分別為：
；
該團隊判定患病白鼠服藥后這項指標不低于85的確認為藥物有效，否則確認為藥物無效.
（1）已知第一種試驗方案的10個數據的平均數為89，求這組數據的方差；
（2）現需要從已服用乙藥的10只白鼠中隨機抽取7只，記其中服藥有效的只數為
，求的分布列與期望；
（3）該團隊的另一實驗室有1000只白鼠，其中900只為正常白鼠，100只為患病白鼠，每用新研制的甲藥給所有患病白鼠服用一次，患病白鼠中有
變為正常白鼠，但正常白鼠仍有
變為患病白鼠，假設實驗室的所有白鼠都活著且數量不變，且記服用
次甲藥后此實驗室正常白鼠的只數為
.
（i）求
并寫出
與的關系式；
（ii）要使服用甲藥兩次后，該實驗室正常白鼠至少有950只，求最大的正整數
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，已知圓
的參數方程為
（
為參數），以坐標原點為極點，
軸的非負半軸為極軸建立極坐標系，圓
的極坐標方程為
，設圓與圓的公共弦所在直線為
.
（1）求直線的極坐標方程；
（2）若以坐標原點為中心，直線
順時針方向旋轉
后與圓、圓分別在第一象限交于
、
兩點，求
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某面包推出一款新面包，每個面包的成本價為4元，售價為10元，該款面包當天只出一爐（一爐至少15個，至多30個），當天如果沒有售完，剩余的面包以每個2元的價格處理掉，為了確定這一爐面包的個數，該店記錄了這款新面包最近30天的日需求量（單位：個），整理得下表：
（1）根據表中數據可知，頻數
與日需求量
（單位：個）線性相關，求關于的線性回歸方程；
（2）以30天記錄的各日需求量的頻率代替各日需求量的概率，若該店這款新面包出爐的個數為24，記當日這款新面包獲得的總利潤為
（單位：元）.
（ⅰ）若日需求量為15個，求；
（ⅱ）求的分布列及其數學期望.
相關公式：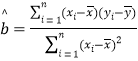
， 
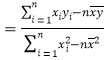查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某次考試，班主任從全班同學中隨機抽取一個容量為8的樣本，他們的數學物理分數對應如下表:
學生編號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
數學分數 | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
物理分數 | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
繪出散點圖如下:
根據以上信息，判斷下列結論:
①根據此散點圖，可以判斷數學成績與物理成績具有線性相關關系；
②根據此散點圖，可以判斷數學成績與物理成績具有一次函數關系；
③甲同學數學考了80分，那么，他的物理成績一定比數學只考了60分的乙同學的物理成績要高.
其中正確的個數為（ ）.
A.0B.3C.2D.1
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，直線
的參數方程為
（
為參數），以坐標原點為極點，
軸的正半軸為極軸建立極坐標系，曲線
的極坐標方程為
．
（Ⅰ）求直線的普通方程和曲線的直角坐標方程；
（Ⅱ）設
為曲線上的點，
，垂足為
，若
的最小值為
，求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某種植園在芒果臨近成熟時，隨機從一些芒果樹上摘下100個芒果，其質量分別在
，
，
，
，
，
（單位：克）中，經統計得頻率分布直方圖如圖所示.
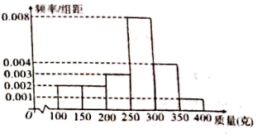
（1）經計算估計這組數據的中位數；
（2）現按分層抽樣從質量為，的芒果中隨機抽取6個，再從這6個中隨機抽取3個，求這3個芒果中恰有1個在內的概率.
（3）某經銷商來收購芒果，以各組數據的中間數代表這組數據的平均值，用樣本估計總體，該種植園中還未摘下的芒果大約還有10000個，經銷商提出如下兩種收購方案：
A：所有芒果以10元/千克收購；
B：對質量低于250克的芒果以2元/個收購，高于或等于250克的以3元/個收購，通過計算確定種植園選擇哪種方案獲利更多？
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】以直角坐標系的原點
為極點，x軸的正半軸為極軸，建立坐標系，兩個坐標系取相同的單位長度．已知直線
的參數方程為
，曲線
的極坐標方程為
（1）求曲線的直角坐標方程
（2）設直線與曲線相交于
兩點，
時，求
的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
