
給出命題:若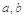 是正常數,且
是正常數,且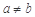 ,
,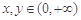 ,則
,則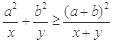 (當且僅當
(當且僅當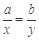 時等號成立).根據上面命題,可以得到函數
時等號成立).根據上面命題,可以得到函數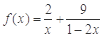 (
(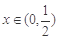 )的最小值及取最小值時的
)的最小值及取最小值時的 值分別為( )
值分別為( )
A.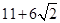 , ,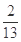 | B.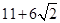 , ,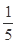 |
C.25,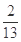 | D.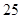 , ,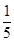 |
科目:高中數學 來源: 題型:單選題
有一段 “三段論”推理是這樣的:對于可導函數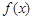 ,若
,若 ,則
,則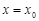 是函數
是函數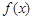 的極值點.因為
的極值點.因為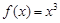 在
在 處的導數值
處的導數值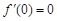 ,所以
,所以 是
是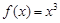 的極值點.以上推理中 ( )
的極值點.以上推理中 ( )
| A.大前提錯誤 | B.小前提錯誤 | C.推理形式錯誤 | D.結論正確 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
用數學歸納法證明1+2+3+ +n2=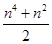 ,則當n=k+1時左端應在n=k的基礎上加上( )
,則當n=k+1時左端應在n=k的基礎上加上( )
| A.k2+1 |
| B.(k+1)2 |
C.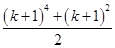 |
| D.(k2+1)+(k2+2)+ +(k+1)2 |
查看答案和解析>>
科目:高中數學 來源: 題型:單選題
用反證法證明命題:“若a,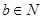 ,
,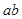 能被5整除,則a,b中至少有一個能被5整除”,那么假設的內容是( )
能被5整除,則a,b中至少有一個能被5整除”,那么假設的內容是( )
| A.a,b都能被5整除 | B.a,b都不能被5整除 |
| C.a,b有一個能被5整除 | D.a,b有一個不能被5整除 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com