
【題目】近幾年一種新奇水果深受廣大消費者的喜愛,一位農(nóng)戶發(fā)揮聰明才智,把這種露天種植的新奇水果搬到了大棚里,收到了很好的經(jīng)濟效益.根據(jù)資料顯示,產(chǎn)出的新奇水果的箱數(shù)x(單位:十箱)與成本y(單位:千元)的關系如下:
x | 1 | 3 | 4 | 6 | 7 |
y | 5 | 6.5 | 7 | 7.5 | 8 |
y與x可用回歸方程![]() ( 其中
( 其中![]() ,
,![]() 為常數(shù))進行模擬.
為常數(shù))進行模擬.
(Ⅰ)若該農(nóng)戶產(chǎn)出的該新奇水果的價格為150元/箱,試預測該新奇水果100箱的利潤是多少元.|.
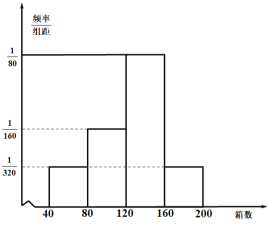
(Ⅱ)據(jù)統(tǒng)計,10月份的連續(xù)16天中該農(nóng)戶每天為甲地配送的該新奇水果的箱數(shù)的頻率分布直方圖如圖所示.
(i)若從箱數(shù)在![]() 內(nèi)的天數(shù)中隨機抽取2天,估計恰有1天的水果箱數(shù)在
內(nèi)的天數(shù)中隨機抽取2天,估計恰有1天的水果箱數(shù)在![]() 內(nèi)的概率;
內(nèi)的概率;
(ⅱ)求這16天該農(nóng)戶每天為甲地配送的該新奇水果的箱數(shù)的平均值.(每組用該組區(qū)間的中點值作代表)
參考數(shù)據(jù)與公式:設![]() ,則
,則
|
|
|
|
0.54 | 6.8 | 1.53 | 0.45 |
線性回歸直線![]() 中,
中, ,
,![]() .
.
【答案】(Ⅰ)6636;(Ⅱ)(i)![]() ;(ⅱ)125箱
;(ⅱ)125箱
【解析】
(Ⅰ)根據(jù)參考數(shù)據(jù)得到![]() 和
和![]() ,代入得到回歸直線方程
,代入得到回歸直線方程![]() ,
,![]() ,
,
再代入![]() 求成本,最后代入利潤公式;
求成本,最后代入利潤公式;
(Ⅱ)(ⅰ)首先分別計算水果箱數(shù)在![]() 和
和![]() 內(nèi)的天數(shù),再用編號列舉基本事件的方法求概率;(ⅱ)根據(jù)頻率分布直方圖直接計算結果.
內(nèi)的天數(shù),再用編號列舉基本事件的方法求概率;(ⅱ)根據(jù)頻率分布直方圖直接計算結果.
(Ⅰ)根據(jù)題意,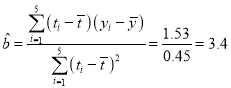 ,
,
所以![]() ,所以
,所以![]() .又
.又![]() ,所以
,所以![]() .
.
所以![]() 時,
時,![]() (千元),
(千元),
即該新奇水果100箱的成本為8364元,故該新奇水果100箱的利潤![]() .
.
(Ⅱ)(i)根據(jù)頻率分布直方圖,可知水果箱數(shù)在![]() 內(nèi)的天數(shù)為
內(nèi)的天數(shù)為![]()
設這兩天分別為a,b,水果箱數(shù)在![]() 內(nèi)的天數(shù)為
內(nèi)的天數(shù)為![]() ,設這四天分別為A,B,C,D,
,設這四天分別為A,B,C,D,
所以隨機抽取2天的基本結果為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共15種.滿足恰有1天的水果箱數(shù)在
,共15種.滿足恰有1天的水果箱數(shù)在![]() 內(nèi)的結果為
內(nèi)的結果為
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共8種,
,共8種,
所以估計恰有1天的水果箱數(shù)在![]() 內(nèi)的概率為
內(nèi)的概率為 ![]() .
.
(ⅱ)這16天該農(nóng)戶每天為甲地配送的該新奇水果的箱數(shù)的平均值為![]() (箱).
(箱).


科目:高中數(shù)學 來源: 題型:
【題目】如圖,在平面直角坐標系![]() 中,已知圓C:
中,已知圓C:![]() ,橢圓E:
,橢圓E:![]() (
(![]() )的右頂點A在圓C上,右準線與圓C相切.
)的右頂點A在圓C上,右準線與圓C相切.
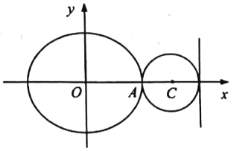
(1)求橢圓E的方程;
(2)設過點A的直線l與圓C相交于另一點M,與橢圓E相交于另一點N.當![]() 時,求直線l的方程.
時,求直線l的方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】[選修4-4:坐標系與參數(shù)方程]
在極坐標系中,O為極點,點![]() 在曲線
在曲線![]() 上,直線l過點
上,直線l過點![]() 且與
且與![]() 垂直,垂足為P.
垂直,垂足為P.
(1)當![]() 時,求
時,求![]() 及l的極坐標方程;
及l的極坐標方程;
(2)當M在C上運動且P在線段OM上時,求P點軌跡的極坐標方程.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】如圖,![]() 是圓
是圓![]() 的直徑,點
的直徑,點![]() 是圓
是圓![]() 上異于
上異于![]() ,
,![]() 的點,直線
的點,直線![]() 平面
平面![]() ,
,![]() ,
,![]() 分別是
分別是![]() ,
,![]() 的中點.
的中點.
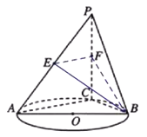
(Ⅰ)記平面![]() 與平面
與平面![]() 的交線為
的交線為![]() ,試判斷直線
,試判斷直線![]() 與平面
與平面![]() 的位置關系,并加以證明;
的位置關系,并加以證明;
(Ⅱ)設![]() ,求二面角
,求二面角![]() 大小的取值范圍.
大小的取值范圍.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)![]() ,函數(shù)
,函數(shù)![]() ,其中
,其中![]() ,
,![]() 是
是![]() 的一個極值點,且
的一個極值點,且![]() .
.
(1)討論![]() 的單調(diào)性
的單調(diào)性
(2)求實數(shù)![]() 和a的值
和a的值
(3)證明![]()
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】“綠水青山就是金山銀山”的生態(tài)文明發(fā)展理念已經(jīng)深入人心,這將推動新能源汽車產(chǎn)業(yè)的迅速發(fā)展,下表是近幾年我國某地區(qū)新能源乘用車的年銷售量與年份的統(tǒng)計表:
年份 | 2014 | 2015 | 2016 | 2017 | 2018 |
銷量(萬臺) | 8 | 10 | 13 | 25 | 24 |
某機構調(diào)查了該地區(qū)30位購車車主的性別與購車種類情況,得到的部分數(shù)據(jù)如下表所示:
購置傳統(tǒng)燃油車 | 購置新能源車 | 總計 | |
男性車主 | 6 | 24 | |
女性車主 | 2 | ||
總計 | 30 |
(1)求新能源乘用車的銷量![]() 關于年份
關于年份![]() 的線性相關系數(shù)
的線性相關系數(shù)![]() ,并判斷
,并判斷![]() 與
與![]() 是否線性相關;
是否線性相關;
(2)請將上述![]() 列聯(lián)表補充完整,并判斷是否有
列聯(lián)表補充完整,并判斷是否有![]() 的把握認為購車車主是否購置新能源乘用車與性別有關;
的把握認為購車車主是否購置新能源乘用車與性別有關;
參考公式: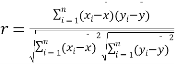 ,
,![]() ,其中
,其中![]() .
.![]() ,若
,若![]() ,則可判斷
,則可判斷![]() 與
與![]() 線性相關.
線性相關.
附表:
| 0.10 | 0.05 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知直線![]() 與拋物線
與拋物線![]() 交于P,Q兩點,且
交于P,Q兩點,且![]() 的面積為16(O為坐標原點).
的面積為16(O為坐標原點).
(1)求C的方程.
(2)直線l經(jīng)過C的焦點F且l不與x軸垂直;l與C交于A,B兩點,若線段AB的垂直平分線與x軸交于點D,試問在x軸上是否存在點E,使![]() 為定值?若存在,求該定值及E的坐標;若不存在,請說明理由.
為定值?若存在,求該定值及E的坐標;若不存在,請說明理由.
查看答案和解析>>
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com