
【題目】已知橢圓![]() 的中心在原點,焦點在坐標軸上,且經過
的中心在原點,焦點在坐標軸上,且經過![]() ,
,![]() .
.
(Ⅰ)求橢圓的標準方程和離心率;
(Ⅱ)四邊形![]() 的四個頂點都在橢圓
的四個頂點都在橢圓![]() 上,且對角線
上,且對角線![]() ,
,![]() 過原點
過原點![]() ,若
,若![]() ,求證:四邊形
,求證:四邊形![]() 的面積為定值,并求出此定值.
的面積為定值,并求出此定值.
 小學課時作業全通練案系列答案
小學課時作業全通練案系列答案 金版課堂課時訓練系列答案
金版課堂課時訓練系列答案 單元全能練考卷系列答案
單元全能練考卷系列答案 新黃岡兵法密卷系列答案
新黃岡兵法密卷系列答案科目:高中數學 來源: 題型:
【題目】如表提供了工廠技術改造后某種型號設備的使用年限![]() 和所支出的維修費
和所支出的維修費![]() (萬元)的幾組對照數據:
(萬元)的幾組對照數據:
| 2 | 3 | 4 | 5 | 6 |
| 1 | 2.5 | 3 | 4 | 4.5 |
參考公式: ,
,![]() .
.
(1)若知道![]() 對
對![]() 呈線性相關關系,請根據上表提供的數據,用最小二乘法求出
呈線性相關關系,請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)已知該工廠技術改造前該型號設備使用10年的維修費用為9萬元,試根據(1)求出的線性回歸方程,預測該型號設備技術改造后,使用10年的維修費用能否比技術改造前降低?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓C:![]() 的離心率為
的離心率為![]() ,左、右頂點分別為A,B,點M是橢圓C上異于A,B的一點,直線AM與y軸交于點P.
,左、右頂點分別為A,B,點M是橢圓C上異于A,B的一點,直線AM與y軸交于點P.
(Ⅰ)若點P在橢圓C的內部,求直線AM的斜率的取值范圍;
(Ⅱ)設橢圓C的右焦點為F,點Q在y軸上,且∠PFQ=90°,求證:AQ∥BM.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在各項均為正數的等比數列{an}中,![]() ,且a4+a5=6a3.
,且a4+a5=6a3.
(Ⅰ)求數列{an}的通項公式;
(Ⅱ)設數列{log2an}的前n項和為Sn,求Sn的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某幼兒園雛鷹班的生活老師統計2018年上半年每個月的20日的晝夜溫差![]() ,
,![]() 和患感冒的小朋友人數(
和患感冒的小朋友人數(![]() /人)的數據如下:
/人)的數據如下:
溫差 |
|
|
|
|
|
|
患感冒人數 | 8 | 11 | 14 | 20 | 23 | 26 |
其中![]() ,
,![]() ,
,![]() .
.
(Ⅰ)請用相關系數加以說明是否可用線性回歸模型擬合![]() 與
與的關系;
(Ⅱ)建立![]() 關于
關于![]() 的回歸方程(精確到
的回歸方程(精確到![]() ),預測當晝夜溫差升高
),預測當晝夜溫差升高![]() 時患感冒的小朋友的人數會有什么變化?(人數精確到整數)
時患感冒的小朋友的人數會有什么變化?(人數精確到整數)
參考數據:![]() .參考公式:相關系數:
.參考公式:相關系數: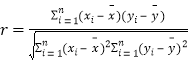 ,回歸直線方程是
,回歸直線方程是![]() ,
,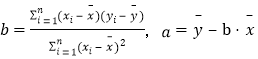 ,
,
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】對給定的d∈N*,記由數列構成的集合![]() .
.
(1)若數列{an}∈Ω(2),寫出a3的所有可能取值;
(2)對于集合Ω(d),若d≥2.求證:存在整數k,使得對Ω(d)中的任意數列{an},整數k不是數列{an}中的項;
(3)已知數列{an},{bn}∈Ω(d),記{an},{bn}的前n項和分別為An,Bn.若|an+1|≤|bn+1|,求證:An≤Bn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某企業生產了一種新產品,在推廣期邀請了100位客戶試用該產品,每人一臺.試用一個月之后進行回訪,由客戶先對產品性能作出“滿意”或“不滿意”的評價,再讓客戶決定是否購買該試用產品(不購買則可以免費退貨,購買則僅需付成本價).經統計,決定退貨的客戶人數是總人數的一半,“對性能滿意”的客戶比“對性能不滿意”的客戶多10人,“對性能不滿意”的客戶中恰有![]() 選擇了退貨.
選擇了退貨.
(1)請完成下面的![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為“客戶購買產品與對產品性能滿意之間有關”.
的把握認為“客戶購買產品與對產品性能滿意之間有關”.
對性能滿意 | 對性能不滿意 | 合計 | |
購買產品 | |||
不購買產品 | |||
合計 |
(2)企業為了改進產品性能,現從“對性能不滿意”的客戶中按是否購買產品進行分層抽樣,隨機抽取6位客戶進行座談.座談后安排了抽獎環節,共有6張獎券,其中一張印有900元字樣,兩張印有600元字樣,三張印有300元字樣,抽到獎券可獲得相應獎金.6位客戶每人隨機抽取一張獎券(不放回),設6位客戶中購買產品的客戶人均所得獎金為![]() 元,求
元,求![]() 的分布列和數學期望.
的分布列和數學期望.
附:![]() ,其中
,其中![]()
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com