【題目】已知函數f(x)＝
在點(1,1)處的切線方程為x＋y＝2.
(1)求a，b的值；
(2)對函數f(x)定義域內的任一個實數x，不等式f(x)－
＜0恒成立，求實數m的取值范圍．
【答案】（1）
（2）m的取值范圍是(1，＋∞).
【解析】試題分析：（1）先根據導數幾何意義得f′(1)＝－1，再根據
解得a，b的值；（2）先變量分離得
最大值，再利用導數研究函數
單調性，進而得最大值，即得實數m的取值范圍．
試題解析：(1)由題f′(x)＝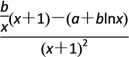
，
又直線x＋y＝2的斜率為－1.2分
∴f′(1)＝－1，即
＝－1.3分
又(1,1)點在函數f(x)＝
的圖象上，
故
＝1，
由
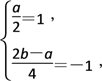解得
(2)由(1)得f(x)＝
(x＞0)，由f(x)＜
及x＞0
＜m，8分
令g(x)＝
g′(x)＝
＝
，
令h(x)＝1－x－ln xh′(x)＝－1－
＜0(x＞0)，故h(x)在區間(0，＋∞)上是減函數，
故當0＜x＜1時，h(x)＞h(1)＝0，
當x＞1時，h(x)＜h(1)＝0.10分
從而當0＜x＜1時，g′(x)＞0，當x＞1時，
g′(x)＜
故g(x)max＝g(1)＝1，要使＜m成立，只需m＞1，
故m的取值范圍是(1，＋∞).
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】定義在R上的偶函數f(x)滿足f(x＋1)＝－f(x)且f(x)在[－1,0]上是增函數，給出下列四個命題：
①f(x)是周期函數；②f(x)的圖象關于x＝1對稱；③f(x)在[1,2]上是減函數；④f(2)＝f(0)．
其中正確命題的序號是____________．(請把正確命題的序號全部寫出來)
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某企業有甲、乙兩套設備生產同一種產品，為了檢測兩套設備的生產質量情況，隨機從兩套設備生產的大量產品中各抽取了50件產品作為樣本，檢測一項質量指標值，若該項質量指標值落在
內，則為合格品，否則為不合格品. 表1是甲套設備的樣本的頻數分布表，圖1是乙套設備的樣本的頻率分布直方圖.
表1：甲套設備的樣本的頻數分布表
質量指標值 | [95,100) | [100,105) | [105,110) | [110,115) | [115,120) | [120,125] |
頻數 | 1 | 4 | 19 | 20 | 5 | 1 |
圖1：乙套設備的樣本的頻率分布直方圖
（1）填寫下面列聯表，并根據列聯表判斷是否有90%的把握認為該企業生產的這種產品的質量指標值與甲、乙兩套設備的選擇有關；
