
【題目】如圖,正四棱錐![]() 的底面邊長為
的底面邊長為![]() ,
,![]() 、
、![]() 分別為
分別為![]() 、
、![]() 的中點.
的中點.
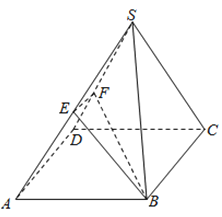
(1)當![]() 時,證明:平面
時,證明:平面![]() 平面
平面![]() ;
;
(2)若平面![]() 與底面
與底面![]() 所成銳二面角為
所成銳二面角為![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
(1)根據四棱錐是正四棱錐,連接![]() 交
交![]() 于點
于點![]() ,以
,以![]() 為原點,以
為原點,以![]() 、
、![]() 、
、![]() 建立空間坐標系.取
建立空間坐標系.取![]() 的中點
的中點![]() ,用向量法證明
,用向量法證明![]() ,
,![]() ,得到
,得到![]() 平面
平面![]() ,再用面面垂直的判定定理證明;
,再用面面垂直的判定定理證明;
(2)設![]() ,求得平面
,求得平面![]() 的一個法向量,取平面
的一個法向量,取平面![]() 的一個法向量,根據平面
的一個法向量,根據平面![]() 與底面
與底面![]() 所成銳二面角為
所成銳二面角為![]() ,由
,由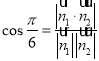 ,求得
,求得![]() ,設直線
,設直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,代入公式
,代入公式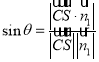 求解.
求解.
(1)連接![]() 交
交![]() 于點
于點![]() ,建立如圖所示空間坐標系.
,建立如圖所示空間坐標系.
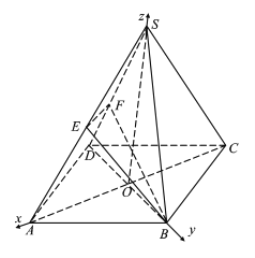
∵![]() ,∴
,∴![]() ,則
,則![]() ,
,![]() ,
,
![]() ,
,![]() ,
,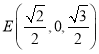 ,
,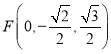 ,
,
設![]() 是
是![]() 的中點,則
的中點,則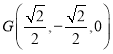 ,
,
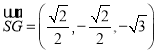 ,
,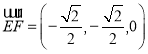 ,
,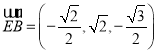 ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
![]() ,∴
,∴![]() 平面
平面![]() ,
,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ;
;
(2)設![]() ,則
,則![]() ,
,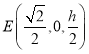 ,
,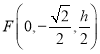 ,
,
則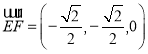 ,
,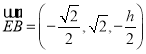 ,
,
設平面![]() 的一個法向量為
的一個法向量為![]() ,則
,則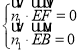 ,即
,即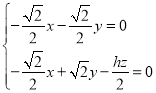 ,
,
令![]() ,則
,則![]() ,
,![]() ,所以
,所以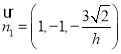 ,
,
取平面![]() 的一個法向量為
的一個法向量為![]() ,
,
則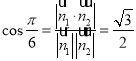 ,即
,即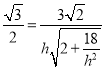 ,解得
,解得![]() ,∴
,∴![]() ,
,
設直線![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ,∴
,∴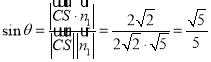 ,
,
即直線![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.


 名師點睛字詞句段篇系列答案
名師點睛字詞句段篇系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() 的最小正周期為
的最小正周期為![]() ,其圖象關于直線
,其圖象關于直線![]() 對稱.給出下面四個結論:①將
對稱.給出下面四個結論:①將![]() 的圖象向右平移
的圖象向右平移![]() 個單位長度后得到函數圖象關于原點對稱;②點
個單位長度后得到函數圖象關于原點對稱;②點![]() 為
為![]() 圖象的一個對稱中心;③
圖象的一個對稱中心;③![]() ;④
;④![]() 在區間
在區間![]() 上單調遞增.其中正確的結論為( )
上單調遞增.其中正確的結論為( )
A.①②B.②③C.②④D.①④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知集合A={(x,y)|(x﹣3﹣4cosq)2+(y﹣5﹣4sinq)2=4,θ∈R},B={(x,y)|3x+4y﹣19=0}.記集合P=A∩B,則集合P所表示的軌跡的長度為( )
A.8![]() B.8
B.8![]() C.8
C.8![]() D.8
D.8![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“未來肯定是非接觸的,無感支付的方式將成為主流,這有助于降低交互門檻”.云從科技聯合創始人姚志強告訴南方日報記者.相對于主流支付方式二維碼支付,刷臉支付更加便利,以前出門一部手機解決所有,而現在連手機都不需要了,畢竟,手機支付還需要攜帶手機,打開二維碼也需要時間和手機信號.刷臉支付將會替代手機,成為新的支付方式.某地從大型超市門口隨機抽取50名顧客進行了調查,得到了如下列聯表:
男性 | 女性 | 總計 | |
刷臉支付 | 18 | 25 | |
非刷臉支付 | 13 | ||
總計 | 50 |
(1)請將上面的列聯表補充完整,并判斷是否有95%的把握認為使用刷臉支付與性別有關?
(2)從參加調查且使用刷臉支付的顧客中隨機抽取2人參加抽獎活動,抽獎活動規則如下:
“一等獎”中獎概率為0.25,獎品為10元購物券![]() 張(
張(![]() ,且
,且![]() ),“二等獎”中獎概率0.25,獎品為10元購物券兩張,“三等獎”中獎概率0.5,獎品為10元購物券一張,每位顧客是否中獎相互獨立,記參與抽獎的兩位顧客中獎購物券金額總和為
),“二等獎”中獎概率0.25,獎品為10元購物券兩張,“三等獎”中獎概率0.5,獎品為10元購物券一張,每位顧客是否中獎相互獨立,記參與抽獎的兩位顧客中獎購物券金額總和為![]() 元,若要使
元,若要使![]() 的均值不低于50元,求
的均值不低于50元,求![]() 的最小值.
的最小值.
附: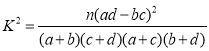 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.010 | 0.005 |
| 2.706 | 3.841 | 6.635 | 7.869 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,(其中
,(其中![]() )的圖象關于點
)的圖象關于點![]() 成中心對稱,且與點
成中心對稱,且與點![]() 相鄰的一個最低點為
相鄰的一個最低點為![]() ,則對于下列判斷:
,則對于下列判斷:
①直線![]() 是函數
是函數![]() 圖象的一條對稱軸;
圖象的一條對稱軸;
②點![]() 是函數
是函數![]() 的一個對稱中心;
的一個對稱中心;
③函數![]() 與
與![]() 的圖象的所有交點的橫坐標之和為
的圖象的所有交點的橫坐標之和為![]() .
.
其中所有正確的判斷是( )
A.①②B.①③C.②③D.②
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】1852年,英國來華傳教士偉烈亞力將《孫子算經》中“物不知數”問題的解法傳至歐洲.1874年,英國數學家馬西森指出此法符合1801年由高斯得到的關于同余式解法的一般性定理,因而西方稱之為“中國剩余定理”.“中國剩余定理”講的是一個關于整除的問題,例如求1到2000這2000個整數中,能被3除余1且被7除余1的數的個數,現由程序框圖,其中MOD函數是一個求余函數,記![]() 表示m除以n的余數,例如
表示m除以n的余數,例如![]() ,則輸出i為( ).
,則輸出i為( ).
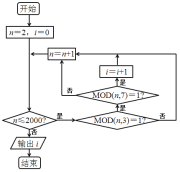
A.98B.97C.96D.95
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,傾斜角為
中,傾斜角為![]() 的直線
的直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).在以坐標原點為極點,
為參數).在以坐標原點為極點,![]() 軸正半軸為極軸的極坐標系中,曲線
軸正半軸為極軸的極坐標系中,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程與曲線
的普通方程與曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 與曲線
與曲線![]() 交于
交于![]() ,
,![]() 兩點,且
兩點,且![]() ,求直線
,求直線![]() 的傾斜角.
的傾斜角.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知點![]() 是橢圓
是橢圓![]() 的右焦點,過點
的右焦點,過點![]() 的直線
的直線![]() 交橢圓于
交橢圓于![]() 兩點,當直線
兩點,當直線![]() 過
過![]() 的下頂點時,
的下頂點時,![]() 的斜率為
的斜率為![]() ,當直線
,當直線![]() 垂直于
垂直于![]() 的長軸時,
的長軸時,![]() 的面積為
的面積為![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)當![]() 時,求直線
時,求直線![]() 的方程;
的方程;
(Ⅲ)若直線![]() 上存在點
上存在點![]() 滿足
滿足![]() 成等比數列,且點
成等比數列,且點![]() 在橢圓外,證明:點
在橢圓外,證明:點![]() 在定直線上.
在定直線上.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】生活中人們常用“通五經貫六藝”形容一個人才識技藝過人,這里的“六藝”其實源于中國周朝的貴族教育體系,具體包括“禮、樂、射、御、書、數”.為弘揚中國傳統文化,某校在周末學生業余興趣活動中開展了“六藝”知識講座,每藝安排一節,連排六節,則滿足“數”必須排在前兩節,“禮”和“樂”必須分開安排的概率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com