
���}Ŀ����֪?ji��ng)��c(di��n)![]() �����c(di��n)
�����c(di��n)![]() �ľ��x��
�ľ��x��![]() ����ֱ��(xi��n)
����ֱ��(xi��n)![]() �ľ��xС1.
�ľ��xС1.
�������c(di��n)![]() ��܉�E
��܉�E![]() �ķ��̣�
�ķ��̣�
�����^(gu��)�c(di��n)![]() ���������ഹֱ�ăɗlֱ��(xi��n)
���������ഹֱ�ăɗlֱ��(xi��n)![]() ���քe������(xi��n)
���քe������(xi��n)![]() ���c(di��n)
���c(di��n)![]() ��
��![]() .�O(sh��)��(xi��n)��
.�O(sh��)��(xi��n)��![]() ��
�� ![]() �����c(di��n)�քe��
�����c(di��n)�քe��![]() �����C��ֱ��(xi��n)
�����C��ֱ��(xi��n)![]() ���^(gu��)һ��(g��)���c(di��n)��
���^(gu��)һ��(g��)���c(di��n)��
�����ڣ��ėl���£���![]() ��e����Сֵ.
��e����Сֵ.
���𰸡���1��![]() ��2���^(gu��)���c(di��n)
��2���^(gu��)���c(di��n)![]() ����3��4
����3��4
��������ԇ�}�����������Ƚ������タ(xi��n)���x�_������(xi��n)���Π��ǒ��タ(xi��n)���ٴ_������(sh��)![]() ���M(j��n)�����
���M(j��n)�����![]() ������������(j��)���ĽY(ji��)Փ�քe����
������������(j��)���ĽY(ji��)Փ�քe����![]() �ķ��̣��ٷքe�c���タ(xi��n)(li��n)�����̽M����������c(di��n)��
�ķ��̣��ٷքe�c���タ(xi��n)(li��n)�����̽M����������c(di��n)��![]() ������(bi��o)��������б�ʵ�׃���_��ֱ��(xi��n)
������(bi��o)��������б�ʵ�׃���_��ֱ��(xi��n)![]() ��(j��ng)�^(gu��)���c(di��n)�������ڣ���ǰ��l���£������
��(j��ng)�^(gu��)���c(di��n)�������ڣ���ǰ��l���£������![]() ��Ȼ����
��Ȼ����![]() ��e�P(gu��n)��׃��
��e�P(gu��n)��׃��![]() �ĺ���(sh��)
�ĺ���(sh��)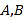 �����\(y��n)�û�������ʽ������Сֵ��
�����\(y��n)�û�������ʽ������Сֵ��
�⣺�������}���֪����(d��ng)�c(di��n)![]() �����c(di��n)
�����c(di��n)![]() �ľ��x����
�ľ��x����![]() ����ֱ��(xi��n)
����ֱ��(xi��n)![]() �ľ��x.����(j��)���タ(xi��n)�Ķ��x��֪���c(di��n)
�ľ��x.����(j��)���タ(xi��n)�Ķ��x��֪���c(di��n)![]() ��܉�E
��܉�E![]() �ǒ��タ(xi��n).
�ǒ��タ(xi��n).
��![]() �������タ(xi��n)���̞飺
�������タ(xi��n)���̞飺 ![]()
�����O(sh��)![]() ���c(di��n)����(bi��o)�քe��
���c(di��n)����(bi��o)�քe��![]() ���t�c(di��n)
���t�c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() .
.
���}����O(sh��)ֱ��(xi��n)![]() �ķ��̞�
�ķ��̞�![]() .
.
��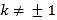 ����
����![]() .
.
![]() .
.
��?y��n)�ֱ��(xi��n)![]() �c����(xi��n)
�c����(xi��n)![]() ��
��![]() ���c(di��n)������
���c(di��n)������![]() .
.
�����c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() .
.
���}֪��ֱ��(xi��n)![]() ��б�ʞ�
��б�ʞ�![]() ��ͬ���ɵ��c(di��n)
��ͬ���ɵ��c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() .
.
��(d��ng)![]() �r(sh��)����
�r(sh��)����![]() ���˕r(sh��)ֱ��(xi��n)
���˕r(sh��)ֱ��(xi��n)![]() ��б��
���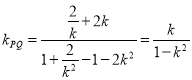 .
.
���ԣ�ֱ��(xi��n)![]() �ķ��̞�
�ķ��̞�![]() ��������
��������![]() .
.
���ǣ�ֱ��(xi��n)![]() ���^(gu��)���c(di��n)
���^(gu��)���c(di��n)![]() ��
��
��(d��ng)![]() �r(sh��)��ֱ��(xi��n)
�r(sh��)��ֱ��(xi��n)![]() �ķ��̞�
�ķ��̞�![]() ��Ҳ�^(gu��)�c(di��n)
��Ҳ�^(gu��)�c(di��n)![]() .
.
�C��������ֱ��(xi��n)![]() ���^(gu��)���c(di��n)
���^(gu��)���c(di��n)![]() .
.
�������![]() .����
.����![]() ��e
��e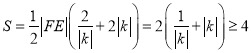 .
.
��(d��ng)�҃H��(d��ng)![]() �r(sh��)����
�r(sh��)����![]() ������������
������������![]() ��e����Сֵ��4.
��e����Сֵ��4.



| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
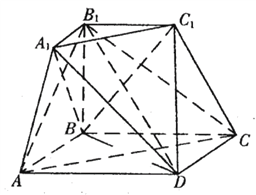
���}Ŀ�������_(t��i)���^(gu��)�c(di��n)![]() ��ƽ���ȥһ���ֺ�õ���D��ʾ�Ď��w�����µ�����߅��
��ƽ���ȥһ���ֺ�õ���D��ʾ�Ď��w�����µ�����߅��![]() ��߅�L(zh��ng)��2�����Σ�
��߅�L(zh��ng)��2�����Σ�![]() ��
��![]() ƽ��
ƽ��![]() ��
��![]() .
.
�������C��ƽ��![]() ƽ��
ƽ��![]() ��
��
������![]() �c����
�c����![]() ���ɽǵ�����ֵ��2��������
���ɽǵ�����ֵ��2��������![]() ������ֵ.
������ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)![]() ��
��![]() .
.
(1)ӑՓ����(sh��)![]() �Ć��{(di��o)�ԣ�
�Ć��{(di��o)�ԣ�
(2)������(sh��)![]() ��
��![]() �ϵ����ֵ��1����(sh��)��(sh��)
�ϵ����ֵ��1����(sh��)��(sh��)![]() ��ȡֵ����.
��ȡֵ����.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪![]() �ǒ��タ(xi��n)
�ǒ��タ(xi��n)![]() �ϵăɂ�(g��)�c(di��n)���c(di��n)
�ϵăɂ�(g��)�c(di��n)���c(di��n)![]() ������(bi��o)��
������(bi��o)��![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() ��б�ʞ�
��б�ʞ�![]() .�O(sh��)���タ(xi��n)
.�O(sh��)���タ(xi��n)![]() �Ľ��c(di��n)��ֱ��(xi��n)
�Ľ��c(di��n)��ֱ��(xi��n)![]() ���·�.
���·�.
��������k��ȡֵ������
�������O(sh��)C��W��һ�c(di��n)����![]() ���^(gu��)
���^(gu��)![]() ���c(di��n)�քe��W���о�(xi��n)��ӛ���о�(xi��n)�Ľ��c(di��n)��
���c(di��n)�քe��W���о�(xi��n)��ӛ���о�(xi��n)�Ľ��c(di��n)��![]() . �Д���߅��
. �Д���߅��![]() �Ƿ�����Σ����f(shu��)������.
�Ƿ�����Σ����f(shu��)������.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪?ji��ng)��c(di��n)![]() �����c(di��n)
�����c(di��n)![]() �ľ��x��
�ľ��x��![]() ����ֱ��(xi��n)
����ֱ��(xi��n)![]() �ľ��xС1.
�ľ��xС1.
�������c(di��n)![]() ��܉�E
��܉�E![]() �ķ��̣�
�ķ��̣�
�����^(gu��)�c(di��n)![]() ���������ഹֱ�ăɗlֱ��(xi��n)
���������ഹֱ�ăɗlֱ��(xi��n)![]() ���քe������(xi��n)
���քe������(xi��n)![]() ���c(di��n)
���c(di��n)![]() ��
��![]() .�O(sh��)��(xi��n)��
.�O(sh��)��(xi��n)��![]() ��
�� ![]() �����c(di��n)�քe��
�����c(di��n)�քe��![]() �����C��ֱ��(xi��n)
�����C��ֱ��(xi��n)![]() ���^(gu��)һ��(g��)���c(di��n)��
���^(gu��)һ��(g��)���c(di��n)��
�����ڣ��ėl���£���![]() ��e����Сֵ.
��e����Сֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ���x��4��4������(bi��o)ϵ�c����(sh��)����
��ƽ��ֱ������(bi��o)ϵ��,������(bi��o)ԭ�c(di��n)��O�c(di��n),![]() �S�������S��O�S�����O����(bi��o)ϵ,��֪����(xi��n)
�S�������S��O�S�����O����(bi��o)ϵ,��֪����(xi��n)![]() �ĘO����(bi��o)���̞�
�ĘO����(bi��o)���̞�![]() ���^(gu��)�c(di��n)
���^(gu��)�c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �ą���(sh��)���̞�
�ą���(sh��)���̞�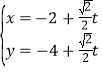 ��
��![]() �酢��(sh��)����ֱ��(xi��n)
�酢��(sh��)����ֱ��(xi��n)![]() �c����(xi��n)
�c����(xi��n)![]() �ཻ��
�ཻ��![]() ���c(di��n).
���c(di��n).
(1)��(xi��)������(xi��n)![]() ��ֱ������(bi��o)���̺�ֱ��(xi��n)
��ֱ������(bi��o)���̺�ֱ��(xi��n)![]() ����ͨ����;
����ͨ����;
(2)��![]() ,��
,��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����ƽ��ֱ������(bi��o)ϵ![]() �У��E�A
�У��E�A![]() �����ҽ��c(di��n)�քe��
�����ҽ��c(di��n)�քe��![]() �x���ʞ�
�x���ʞ�![]() ���ɜ�(zh��n)��(xi��n)֮�g�ľ��x��8,�c(di��n)
���ɜ�(zh��n)��(xi��n)֮�g�ľ��x��8,�c(di��n)![]() �ڙE�A
�ڙE�A![]() �ϣ���λ�ڵ�һ���ޣ��^(gu��)�c(di��n)
�ϣ���λ�ڵ�һ���ޣ��^(gu��)�c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �Ĵ���(xi��n)
�Ĵ���(xi��n)![]() ���^(gu��)�c(di��n)
���^(gu��)�c(di��n)![]() ��ֱ��(xi��n)
��ֱ��(xi��n)![]() �Ĵ���(xi��n)
�Ĵ���(xi��n)![]() ��
��
��1����E�A![]() �Ę�(bi��o)��(zh��n)���̣�
�Ę�(bi��o)��(zh��n)���̣�
��2����ֱ��(xi��n)![]() �Ľ��c(di��n)
�Ľ��c(di��n)![]() �ڙE�A
�ڙE�A![]() �������c(di��n)
�������c(di��n)![]() ������(bi��o)��
������(bi��o)��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪�A![]() �cֱ��(xi��n)
�cֱ��(xi��n)![]() ����.
����.
��1����ֱ��(xi��n)![]() �c�A
�c�A![]() ����
����![]() ���c(di��n)����
���c(di��n)����![]() ��
��
��2���O(sh��)�A![]() �c
�c![]() �S��ؓ(f��)���S�Ľ��c(di��n)��
�S��ؓ(f��)���S�Ľ��c(di��n)��![]() ���^(gu��)�c(di��n)
���^(gu��)�c(di��n)![]() ���ɗlб�ʷքe��
���ɗlб�ʷքe��![]() ��ֱ��(xi��n)���A
��ֱ��(xi��n)���A![]() ��
��![]() ���c(di��n)����
���c(di��n)����![]() ��ԇ�C��ֱ��(xi��n)
��ԇ�C��ֱ��(xi��n)![]() ���^(gu��)һ���c(di��n)�������ԓ���c(di��n)������(bi��o).
���^(gu��)һ���c(di��n)�������ԓ���c(di��n)������(bi��o).
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�
���}Ŀ����֪����(sh��)f��x��=axlnx��x+l ��a��R������f��x����0��
��I����a��
�� II�����C����(d��ng)��n��N*�r(sh��)�� ![]()
�鿴�𰸺ͽ���>>
��(gu��)�H�W(xu��)У��(y��u)�x - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | ����p�_�e��(b��o)��(zhu��n)�^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)��(zhu��n)�^(q��) | �����֙�(qu��n)�e��(b��o)��(zhu��n)�^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ(hu��)��027-86699610 �e��(b��o)�]�䣺58377363@163.com