
【題目】給定橢圓![]()
![]() ,稱圓心在原點
,稱圓心在原點![]() ,半徑為
,半徑為![]() 的圓是橢圓
的圓是橢圓![]() 的“準圓”.若橢圓
的“準圓”.若橢圓![]() 的一個焦點為
的一個焦點為![]() ,其短軸上的一個端點到
,其短軸上的一個端點到![]() 的距離為
的距離為![]() .
.
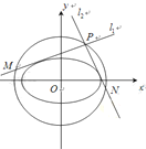
(1)求橢圓![]() 的方程和其“準圓”方程;
的方程和其“準圓”方程;
(2)點![]() 是橢圓
是橢圓![]() 的“準圓”上的動點,過點
的“準圓”上的動點,過點![]() 作橢圓的切線
作橢圓的切線![]() 交“準圓”于點
交“準圓”于點![]() .
.
①當點![]() 為“準圓”與
為“準圓”與![]() 軸正半軸的交點時,求直線
軸正半軸的交點時,求直線![]() 的方程并證明
的方程并證明![]() ;
;
②求證:線段![]() 的長為定值.
的長為定值.
【答案】(1)橢圓方程為![]() ,準圓方程為
,準圓方程為![]() ;(2)①
;(2)①![]() ,證明見解析;②證明見解析
,證明見解析;②證明見解析
【解析】
(1)根據題意![]() ,得到橢圓方程和準圓方程.
,得到橢圓方程和準圓方程.
(2)(ⅰ)設直線為![]() ,聯立方程計算
,聯立方程計算![]() 得到
得到![]() ,得到答案.
,得到答案.
(ⅱ)考慮斜率存在和不存在兩種情況,設點![]() ,切線為
,切線為![]() ,聯立方程得到
,聯立方程得到![]() ,
,![]() ,得到直線
,得到直線![]() 垂直,得到線段
垂直,得到線段![]() 為準圓的直徑,得到答案.
為準圓的直徑,得到答案.
(1)![]() ,
,![]() 橢圓方程為
橢圓方程為![]() ,準圓方程為
,準圓方程為![]() .
.
(2)(ⅰ)因為準圓![]() 與
與![]() 軸正半軸的交點為
軸正半軸的交點為![]() ,
,
設過點![]() 且與橢圓相切的直線為
且與橢圓相切的直線為![]() ,
,
所以由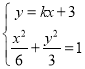 得
得![]() .
.
因為直線![]() 與橢圓相切,所以
與橢圓相切,所以![]() ,解得
,解得![]() ,
,
所以![]() 方程為
方程為![]() ,
,![]() ,
,![]() .
.
(ⅱ)①當直線![]() 中有一條斜率不存在時,不妨設直線
中有一條斜率不存在時,不妨設直線![]() 斜率不存在,
斜率不存在,
則![]() :
:![]() ,當
,當![]() :
:![]() 時,
時,![]() 與準圓交于點
與準圓交于點![]() ,
,
此時![]() 為
為![]() (或
(或![]() ),顯然直線
),顯然直線![]() 垂直;
垂直;
同理可證當![]() :
:![]() 時,直線
時,直線![]() 垂直
垂直
②當![]() 斜率存在時,設點
斜率存在時,設點![]() ,其中
,其中![]() .
.
設經過點![]() 與橢圓相切的直線為
與橢圓相切的直線為![]() ,
,
所以由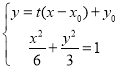 得
得![]() .
.
由![]() 化簡整理得
化簡整理得![]() ,
,
因為![]() ,所以有
,所以有![]() .
.
設![]() 的斜率分別為
的斜率分別為![]() ,因為
,因為![]() 與橢圓相切,
與橢圓相切,
所以![]() 滿足上述方程
滿足上述方程![]() ,
,
所以![]() ,即
,即![]() 垂直.
垂直.
綜合①②知:因為![]() 經過點
經過點![]() ,又分別交其準圓于點
,又分別交其準圓于點![]() ,且
,且![]() 垂直.
垂直.
所以線段![]() 為準圓
為準圓![]() 的直徑,
的直徑,![]() ,
,
所以線段![]() 的長為定值6.
的長為定值6.


科目:高中數學 來源: 題型:
【題目】2019年全國“兩會”,即中華人民共和國第十三屆全國人大二次會議和中國人民政治協商會議第十三屆全國會第二次會議,分別于2019年3月5日和3月3日在北京召開.為了了解哪些人更關注“兩會”,某機構隨機抽取了年齡在![]() 歲之間的200人進行調查,并按年齡繪制出頻率分布直方圖,如圖.
歲之間的200人進行調查,并按年齡繪制出頻率分布直方圖,如圖.
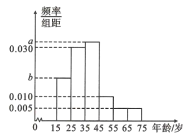
若把年齡在區間![]() ,
,![]() 內的人分別稱為“青少年”“中老年”.經統計“青少年”和“中老年”的人數之比為
內的人分別稱為“青少年”“中老年”.經統計“青少年”和“中老年”的人數之比為![]() .其中“青少年”中有40人關注“兩會”,“中老年”中關注“兩會”和不關注“兩會”的人數之比為
.其中“青少年”中有40人關注“兩會”,“中老年”中關注“兩會”和不關注“兩會”的人數之比為![]() .
.
(1)求圖中![]() 的值.
的值.
(2)現采用分層抽樣在![]() 和
和![]() 中隨機抽取8人作為代表,從8人中任選2人,求2人都是“中老年”的概率.
中隨機抽取8人作為代表,從8人中任選2人,求2人都是“中老年”的概率.
(3)根據已知條件,完成下面的![]() 列聯表,并判斷能否有
列聯表,并判斷能否有![]() %的把握認為“中老年”比“青少年”更加關注“兩會”.
%的把握認為“中老年”比“青少年”更加關注“兩會”.
關注 | 不關注 | 總計 | |
“青少年” | |||
“中老年” | |||
總計 |
附: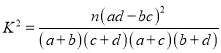 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)=|x﹣a|+|x+b|,ab>0.
(1)當a=1,b=1時,求不等式f(x)<3的解集;
(2)若f(x)的最小值為2,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】上世紀末河南出土的以鶴的尺骨(翅骨)制成的“骨笛”(圖1),充分展示了我國古代高超的音律藝術及先進的數學水平,也印證了我國古代音律與歷法的密切聯系.圖2為骨笛測量“春(秋)分”,“夏(冬)至”的示意圖,圖3是某骨笛的部分測量數據(骨笛的彎曲忽略不計),夏至(或冬至)日光(當日正午太陽光線)與春秋分日光(當日正午太陽光線)的夾角等于黃赤交角.


由歷法理論知,黃赤交角近1萬年持續減小,其正切值及對應的年代如下表:
黃赤交角 |
|
|
|
|
|
正切值 | 0.439 | 0.444 | 0.450 | 0.455 | 0.461 |
年代 | 公元元年 | 公元前2000年 | 公元前4000年 | 公元前6000年 | 公元前8000年 |
根據以上信息,通過計算黃赤交角,可估計該骨笛的大致年代是( )
A.公元前2000年到公元元年B.公元前4000年到公元前2000年
C.公元前6000年到公元前4000年D.早于公元前6000年
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某中學長期堅持貫徹以人為本,因材施教的教育理念,每年都會在校文化節期間舉行“數學素養能力測試”和“語文素養能力測試”兩項測試,以給學生課外興趣學習及輔導提供參考依據.成績分為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 五個等級(等級
五個等級(等級![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 分別對應5分,4分,3分,2分,1分).某班學生兩科的考試成績的數據統計如圖所示,其中“語文素養能力測試”科目的成績為
分別對應5分,4分,3分,2分,1分).某班學生兩科的考試成績的數據統計如圖所示,其中“語文素養能力測試”科目的成績為![]() 的考生有3人.
的考生有3人.
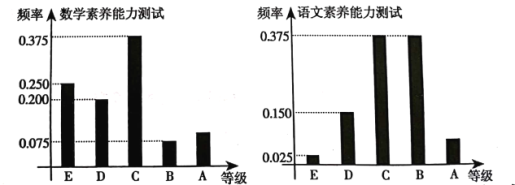
(1)求該班“數學素養能力測試”的科目平均分以及“數學素養能力測試”科目成績為![]() 的人數;
的人數;
(2)若該班共有9人得分大于7分,其中有2人10分,3人9分,4人8分.從這9人中隨機抽取三人,設三人的成績之和為![]() ,求
,求![]() .
.
(3)從該班得分大于7分的9人中選3人即甲,乙,丙組隊參加學校內的“數學限時解題挑戰賽”.規則為:每隊首先派一名隊員參加挑戰賽,在限定的時間,若該生解決問題,即團隊挑戰成功,結束挑戰;若解決問題失敗,則派另外一名隊員上去挑戰,直至派完隊員為止.通過訓練,已知甲,乙,丙通過挑戰賽的概率分別是![]() ,
,![]() ,
,![]() ,問以怎樣的先后順序派出隊員,可使得派出隊員數目的均值達到最小?(只需寫出結果)
,問以怎樣的先后順序派出隊員,可使得派出隊員數目的均值達到最小?(只需寫出結果)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 為等差數列,且
為等差數列,且![]() ,
,![]()
(Ⅰ)求數列![]() 的通項
的通項![]() ,及前
,及前![]() 項和
項和![]()
(Ⅱ)請你在數列![]() 的前4項中選出三項,組成公比的絕對值小于1的等比數列
的前4項中選出三項,組成公比的絕對值小于1的等比數列![]() 的前3項,并記數列
的前3項,并記數列![]() 的前n項和為
的前n項和為![]() .若對任意正整數
.若對任意正整數![]() ,不等式
,不等式![]() 恒成立,試求
恒成立,試求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的標準方程是
的標準方程是![]() ,設
,設![]() 是橢圓
是橢圓![]() 的左焦點,
的左焦點,![]() 為直線
為直線![]() 上任意一點,過
上任意一點,過![]() 做
做![]() 的垂線交橢圓
的垂線交橢圓![]() 于點
于點![]() ,
,![]() .
.
(1)證明:線段![]() 平分線段
平分線段![]() (其中
(其中![]() 為坐標原點);
為坐標原點);
(2)當![]() 最小時,求點
最小時,求點![]() 的坐標.
的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為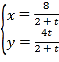 (
(![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若射線![]() (
(![]() )與直線
)與直線![]() 和曲線
和曲線![]() 分別交于
分別交于![]() ,
,![]() 兩點,求
兩點,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com