
【題目】四川省雙流中學是一所國家級示范高中,具有悠久的辦學歷史、豐富的辦學經驗.近年來,雙中共為國內外高校輸送合格新生20000余名,其中為清華、北大、復旦、人大等一流學府輸送新生1800余名,上本科線人數年年超過千人,培養出省、市、縣高考冠軍17名,位居成都市同類學校前茅.該校高三某班有50名學生參加了今年成都市“一診”考試,其中英語成績服從正態分布![]() ,數學成績的頻率分布直方圖如下:
,數學成績的頻率分布直方圖如下:
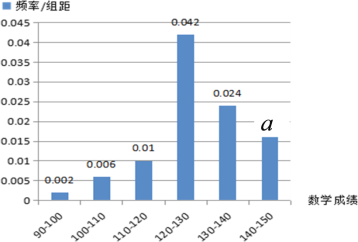
(1)如果成績140分及以上為單科特優,則該班本次考試中英語、數學單科特優大約各多少人?
(2)試問該班本次考試中英語和數學平均成績哪個較高,并說明理由;
(3)如果英語和數學兩科都為單科特優共有5人,把(1)中的近似數作為真實值,從(1)中這些同學中隨機抽取3人,設三人中英語和數學雙科特優的有![]() 人,求
人,求![]() 的分布列和數學期望.
的分布列和數學期望.
參考公式及數據:
![]() 則
則
![]()
![]()
![]()
【答案】(1)英語有![]() 人,數學有
人,數學有![]() 人;(2)數學,理由見解析;(3)分布列見解析,
人;(2)數學,理由見解析;(3)分布列見解析,![]()
【解析】
(1)由英語成績服從正態分布![]() ,求出英語成績為單科特優的概率為
,求出英語成績為單科特優的概率為![]() ,由此能求出英語成績為單科特優的同學的人數,由圖形先求出
,由此能求出英語成績為單科特優的同學的人數,由圖形先求出![]() ,由此能求出數學成績特優的同學的人數;
,由此能求出數學成績特優的同學的人數;
(2)英語的平均價成績為120人,數學的平均成績為127分,從而數學的平均成績更高;
(3)英語和數學雙科特優的有5人,單科特優的有8人,得到![]() 的取值為
的取值為![]() ,分別求出相應的概率,由此求得隨機變量
,分別求出相應的概率,由此求得隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
(1)由題意,英語成績服從正態分布![]() ,
,
所以英語成績為單科特優的概率為![]() ,
,
所以英語成績為單科特優的同學約有![]() 人,
人,
因為![]() ,解得
,解得![]()
數學成績特別優秀的同學約有![]() 人.
人.
(2)英語的平均成績為120分,
數學的平均成績為![]() 分,
分,
因為![]() ,所以數學的平均成績更高.
,所以數學的平均成績更高.
(3)英語和數學雙科特優的有5人,單科特優的有8人,
從中抽取3人,隨機變量![]() 可能取值有0,1,2,3,
可能取值有0,1,2,3,
![]() ;
;![]() ;
;
![]() ;
;![]()
故![]() 的分布列為:
的分布列為:
| 0 | 1 | 2 | 3 |
|
|
|
|
|
所以![]() 的數學期望為
的數學期望為![]() (人).
(人).


 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:高中數學 來源: 題型:
【題目】“二進制”來源于我國古代的《易經》,該書中有兩類最基本的符號:“—”和“——”,其中“—”在二進制中記作“1”,“——”在二進制中記作“0”,例如二進制數![]() 化為十進制的計算如下:
化為十進制的計算如下:![]() .若從兩類符號中任取2個符號進行排列,則得到的二進制數所對應的十進制數大于2的概率為( )
.若從兩類符號中任取2個符號進行排列,則得到的二進制數所對應的十進制數大于2的概率為( )
A.0B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】[選修4-4:坐標系與參數方程]
在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),直線
為參數),直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(1)求![]() 和
和![]() 的直角坐標方程;
的直角坐標方程;
(2)若曲線![]() 截直線
截直線![]() 所得線段的中點坐標為
所得線段的中點坐標為![]() ,求
,求![]() 的斜率.
的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】新疆小南瓜以沙甜聞名全國,小田計劃從新疆運輸小南瓜去上海,隨機從某瓜農的瓜地里挑選了100個,其質量分別在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (單位:克)中,經統計得頻率分布直方圖如圖所示,將頻率視為概率.
(單位:克)中,經統計得頻率分布直方圖如圖所示,將頻率視為概率.
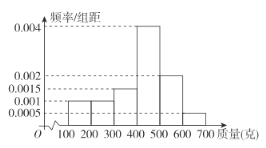
(1)請根據頻率分布直方圖估計該瓜農的小南瓜的平均質量;
(2)已知瓜地里還有2萬個小南瓜已經成熟,可以采摘,小田想全部購買,可是瓜農要求超過400克的小南瓜以5元一個的價格出售,其他的以3元一個的價格出售.將頻率視為概率,若新疆到上海往返的運費約2000元,請問這2萬個小南瓜在上海以每斤(500克)多少元定價才能保證小田的利潤不少于5000元?(結果保留一位小數)
(3)某天王阿姨在上海某超市的蔬菜柜臺上看到小田從新疆采摘的新疆小南瓜,已知柜臺上有若干個,若質量超過500克的小南瓜為“優質品”,王阿姨隨機購買了20個小南瓜,求王阿姨購買的小南瓜中“優質品”個數的期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某校![]() 名學生參加軍事冬令營活動,活動期間各自扮演一名角色進行分組游戲,角色按級別從小到大共
名學生參加軍事冬令營活動,活動期間各自扮演一名角色進行分組游戲,角色按級別從小到大共![]() 種,分別為士兵、排長、連長、營長、團長、旅長、師長、軍長和司令.游戲分組有兩種方式,可以
種,分別為士兵、排長、連長、營長、團長、旅長、師長、軍長和司令.游戲分組有兩種方式,可以![]() 人一組或者
人一組或者![]() 人一組.如果
人一組.如果![]() 人一組,則必須角色相同;如果
人一組,則必須角色相同;如果![]() 人一組,則
人一組,則![]() 人角色相同或者
人角色相同或者![]() 人為級別連續的
人為級別連續的![]() 個不同角色.已知這
個不同角色.已知這![]() 名學生扮演的角色有
名學生扮演的角色有![]() 名士兵和
名士兵和![]() 名司令,其余角色各
名司令,其余角色各![]() 人,現在新加入
人,現在新加入![]() 名學生,將這
名學生,將這![]() 名學生分成
名學生分成![]() 組進行游戲,則新加入的學生可以扮演的角色的種數為________.
組進行游戲,則新加入的學生可以扮演的角色的種數為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)解關于![]() 的不等式:
的不等式:![]() ;
;
(2)當![]() 時,過點
時,過點![]() 是否存在函數
是否存在函數![]() 圖象的切線?若存在,有多少條?若不存在,說明理由;
圖象的切線?若存在,有多少條?若不存在,說明理由;
(3)若![]() 是使
是使![]() 恒成立的最小值,試比較
恒成立的最小值,試比較![]() 與
與![]() 的大小(
的大小(![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,分別過橢圓![]() 左、右焦點
左、右焦點![]() 的動直線
的動直線![]() 相交于
相交于![]() 點,與橢圓
點,與橢圓![]() 分別交于
分別交于![]() 與
與![]() 不同四點,直線
不同四點,直線![]() 的斜率
的斜率![]() 滿足
滿足![]() .已知當
.已知當![]() 與
與![]() 軸重合時,
軸重合時,![]() ,
,![]() .
.
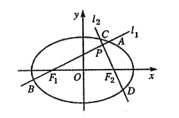
(Ⅰ)求橢圓![]() 的方程;
的方程;
(Ⅱ)是否存在定點![]() ,使得
,使得![]() 為定值?若存在,求出
為定值?若存在,求出![]() 點坐標并求出此定值;若不存在,說明理由.
點坐標并求出此定值;若不存在,說明理由.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() ,
,![]() 和
和![]() .
.
【解析】試題分析:(1)當![]() 與
與![]() 軸重合時,
軸重合時,![]() 垂直于
垂直于![]() 軸,得
軸,得![]() ,得
,得![]() ,
,![]() 從而得橢圓的方程;(2)由題目分析如果存兩定點,則
從而得橢圓的方程;(2)由題目分析如果存兩定點,則![]() 點的軌跡是橢圓或者雙曲線 ,所以把
點的軌跡是橢圓或者雙曲線 ,所以把![]() 坐標化,可得
坐標化,可得![]() 點的軌跡是橢圓,從而求得定點
點的軌跡是橢圓,從而求得定點![]() 和點
和點![]() .
.
試題解析:![]() 當
當![]() 與
與![]() 軸重合時,
軸重合時,![]() , 即
, 即![]() ,所以
,所以![]() 垂直于
垂直于![]() 軸,得
軸,得![]() ,
,![]() ,, 得
,, 得![]() ,
,![]() 橢圓
橢圓![]() 的方程為
的方程為![]() .
.
![]() 焦點
焦點![]() 坐標分別為
坐標分別為![]() , 當直線
, 當直線![]() 或
或![]() 斜率不存在時,
斜率不存在時,![]() 點坐標為
點坐標為![]() 或
或![]() ;
;
當直線![]()
![]() 斜率存在時,設斜率分別為
斜率存在時,設斜率分別為![]() , 設
, 設![]()
![]() 由
由 , 得:
, 得:
![]() , 所以:
, 所以:![]() ,
,![]() , 則:
, 則:
![]()
![]() . 同理:
. 同理:![]()
![]() , 因為
, 因為
![]() , 所以
, 所以![]()
![]() , 即
, 即![]() , 由題意知
, 由題意知![]() , 所以
, 所以
![]() , 設
, 設![]() ,則
,則![]() ,即
,即![]() ,由當直線
,由當直線![]() 或
或![]() 斜率不存在時,
斜率不存在時,![]() 點坐標為
點坐標為![]() 或
或![]() 也滿足此方程,所以點
也滿足此方程,所以點![]() 在橢圓
在橢圓![]() 上.存在點
上.存在點![]() 和點
和點![]() ,使得
,使得![]() 為定值,定值為
為定值,定值為![]() .
.
考點:圓錐曲線的定義,性質,方程.
【方法點晴】本題是對圓錐曲線的綜合應用進行考查,第一問通過兩個特殊位置,得到基本量![]() ,
,![]() ,得
,得![]() ,
,![]() ,從而得橢圓的方程,第二問由題目分析如果存兩定點,則
,從而得橢圓的方程,第二問由題目分析如果存兩定點,則![]() 點的軌跡是橢圓或者雙曲線 ,本題的關鍵是從這個角度出發,把
點的軌跡是橢圓或者雙曲線 ,本題的關鍵是從這個角度出發,把![]() 坐標化,求得
坐標化,求得![]() 點的軌跡方程是橢圓
點的軌跡方程是橢圓![]() ,從而求得存在兩定點
,從而求得存在兩定點![]() 和點
和點![]() .
.
【題型】解答題
【結束】
21
【題目】已知![]() ,
,![]() ,
,![]() .
.
(Ⅰ)若![]() ,求
,求![]() 的極值;
的極值;
(Ⅱ)若函數![]() 的兩個零點為
的兩個零點為![]() ,記
,記![]() ,證明:
,證明:![]() .
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com