
【題目】設數列![]() 的前
的前![]() 項和為
項和為![]() ,對于任意的
,對于任意的![]() ,都有
,都有![]() .
.
(1)求數列![]() 的首項
的首項![]() 及數列的遞推關系式
及數列的遞推關系式![]() ;
;
(2)若數列![]() 成等比數列,求常數
成等比數列,求常數![]() 的值,并求數列
的值,并求數列![]() 的通項公式;
的通項公式;
(3)數列![]() 中是否存在三項
中是否存在三項![]() 、
、![]() 、
、![]() ,它們組成等差數列?若存在,請求出一組適合條件的項;若不存在,請說明理由.
,它們組成等差數列?若存在,請求出一組適合條件的項;若不存在,請說明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】已知拋物線Γ的準線方程為![]() .焦點為
.焦點為![]() .
.
(1)求證:拋物線Γ上任意一點![]() 的坐標
的坐標![]() 都滿足方程:
都滿足方程:![]()
(2)請求出拋物線Γ的對稱性和范圍,并運用以上方程證明你的結論;
(3)設垂直于![]() 軸的直線與拋物線交于
軸的直線與拋物線交于![]() 兩點,求線段
兩點,求線段![]() 的中點
的中點![]() 的軌跡方程.
的軌跡方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
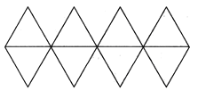
【題目】蹴鞠起源于春秋戰國,是現代足球的前身.到了唐代,制作的蹴鞠已接近于現代足球,做法是:用八片鞣制好的尖皮縫制成“圓形”的球殼,在球殼內放一個動物膀胱,“噓氣閉而吹之”,成為充氣的球.如圖所示,將八個全等的正三角形縫制成一個空間幾何體,在幾何體內放一個氣球,往氣球內充氣使幾何體膨脹,當幾何體膨脹成球體(頂點位置不變)且恰好是原幾何體外接球時,測得球的體積是![]() ,則正三角形的邊長為( )
,則正三角形的邊長為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國家統計局服務業調查中心和中國物流與采購聯合會發布的2018年10月份至2019年9月份共12個月的中國制造業采購經理指數(PMI)如下圖所示.則下列結論中錯誤的是( )
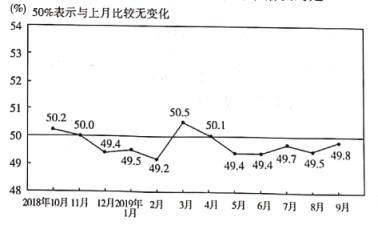
A.12個月的PMI值不低于50%的頻率為![]()
B.12個月的PMI值的平均值低于50%
C.12個月的PMI值的眾數為49.4%
D.12個月的PMI值的中位數為50.3%
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】以直角坐標系xOy的原點為極坐標系的極點,x軸的正半軸為極軸.已知曲線![]() 的極坐標方程為
的極坐標方程為![]() ,P是
,P是![]() 上一動點,
上一動點,![]() ,Q的軌跡為
,Q的軌跡為![]() .
.
(1)求曲線![]() 的極坐標方程,并化為直角坐標方程,
的極坐標方程,并化為直角坐標方程,
(2)若點![]() ,直線l的參數方程為
,直線l的參數方程為![]() (t為參數),直線l與曲線
(t為參數),直線l與曲線![]() 的交點為A,B,當
的交點為A,B,當![]() 取最小值時,求直線l的普通方程.
取最小值時,求直線l的普通方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《算法統宗》全稱《新編直指算法統宗》,是屮國古代數學名著,程大位著.書中有如下問題:“今有五人均銀四十兩,甲得十兩四錢,戊得五兩六錢.問:次第均之,乙丙丁各該若干?”意思是:有5人分40兩銀子,甲分10兩4錢,戊分5兩6錢,且相鄰兩項差相等,則乙丙丁各分幾兩幾錢?(注:1兩等于10錢)( )
A.乙分8兩,丙分8兩,丁分8兩B.乙分8兩2錢,丙分8兩,丁分7兩8錢
C.乙分9兩2錢,丙分8兩,丁分6兩8錢D.乙分9兩,丙分8兩,丁分7兩
查看答案和解析>>
科目:高中數學 來源: 題型:
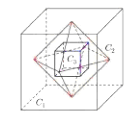
【題目】如圖,記棱長為1的正方體![]() ,以
,以![]() 各個面的中心為頂點的正八面體為
各個面的中心為頂點的正八面體為![]() ,以
,以![]() 各面的中心為頂點的正方體為
各面的中心為頂點的正方體為![]() ,以
,以![]() 各個面的中心為頂點的正八面體為
各個面的中心為頂點的正八面體為![]() ,……,以此類推得一系列的多面體
,……,以此類推得一系列的多面體![]() ,設
,設![]() 的棱長為
的棱長為![]() ,則數列
,則數列![]() 的各項和為________.
的各項和為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() 與曲線
與曲線![]() ,(
,(![]() 為參數).以坐標原點為極點,
為參數).以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)寫出曲線![]() ,
,![]() 的極坐標方程;
的極坐標方程;
(2)在極坐標系中,已知![]() 與
與![]() ,
,![]() 的公共點分別為
的公共點分別為![]() ,
,![]() ,
,![]() ,當
,當![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的左,右焦點分別為
的左,右焦點分別為![]() ,
,![]() ,
,![]() ,M是橢圓E上的一個動點,且
,M是橢圓E上的一個動點,且![]() 的面積的最大值為
的面積的最大值為![]() .
.
(1)求橢圓E的標準方程,
(2)若![]() ,
,![]() ,四邊形ABCD內接于橢圓E,
,四邊形ABCD內接于橢圓E,![]() ,記直線AD,BC的斜率分別為
,記直線AD,BC的斜率分別為![]() ,
,![]() ,求證:
,求證:![]() 為定值.
為定值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com