
【題目】在所有棱長都相等的三棱柱![]() 中,
中,![]() .
.
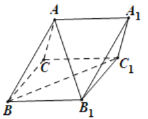
(1)證明:![]() ;
;
(2)若二面角![]() 的大小為
的大小為![]() ,求
,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)證明見解析;(2)![]() .
.
【解析】
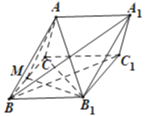
(1) 連![]() ,
,![]() ,取線段
,取線段![]() 的中點(diǎn)
的中點(diǎn)![]() ,連接
,連接![]() 和
和![]() ,再證明
,再證明![]() 平面
平面![]() 即可.
即可.
(2)根據(jù)(1)可知![]() 是二面角
是二面角![]() 的平面角,進(jìn)而找到
的平面角,進(jìn)而找到![]() 與平面
與平面![]() 所成角再求解即可.或者建立空間直角坐標(biāo)系,利用空間向量求解線面角的方法求解.
所成角再求解即可.或者建立空間直角坐標(biāo)系,利用空間向量求解線面角的方法求解.
(Ⅰ)連![]() ,
,![]() ,取線段
,取線段![]() 的中點(diǎn)
的中點(diǎn)![]() ,連接
,連接![]() 和
和![]() ,
,
∵![]() 和
和![]() 為等邊三角形,
為等邊三角形,
∴![]() ,
,![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() .
.
(Ⅱ)法一:∵![]() ,
,![]() ,
,
∴![]() 是二面角
是二面角![]() 的平面角,
的平面角,
∵![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ,
,
記![]() 與
與![]() 的交點(diǎn)為
的交點(diǎn)為![]() ,過
,過![]() 作
作![]() 于
于![]() ,則
,則![]() 平面
平面![]() ,
,
∴![]() 是
是![]() 與平面
與平面![]() 所成角.
所成角.
由題意知![]() 為
為![]() 的重心,
的重心,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,∴
,∴![]() ,
,
∴![]() .
.
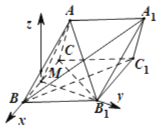
法二:由![]() ,以
,以![]() 為
為![]() 軸,
軸,![]() 為
為![]() 軸,過點(diǎn)
軸,過點(diǎn)![]() 平面
平面![]() 的垂線為
的垂線為![]() 軸,如圖建立空間直角坐標(biāo)系,得
軸,如圖建立空間直角坐標(biāo)系,得
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
, ,
,
則![]() ,
,![]() ,
, ,
,
設(shè)平面![]() 的法向量
的法向量![]() ,
,
則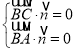 ,得
,得 ,令
,令![]() 得
得![]() ,
,![]() ,
,
則![]() .
.
設(shè)![]() 與平面
與平面![]() 所成角為
所成角為![]() ,
,

![]() ,
,
所以![]() 與平面
與平面![]() 所成角的正弦值為
所成角的正弦值為![]() .
.


 全程金卷系列答案
全程金卷系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知△ABC的內(nèi)角A,B,C的對邊分別為a,b,c,且asinB=bsin(A+![]() ).
).
(1)求A;
(2)若b,![]() a,c成等差數(shù)列,△ABC的面積為2
a,c成等差數(shù)列,△ABC的面積為2![]() ,求a.
,求a.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】(本小題滿分12分)設(shè)函數(shù)![]() .
.
(Ⅰ)若函數(shù)![]() 在定義域上為增函數(shù),求實數(shù)
在定義域上為增函數(shù),求實數(shù)![]() 的取值范圍;
的取值范圍;
(Ⅱ)在(Ⅰ)的條件下,若函數(shù)![]() ,
,![]() 使得
使得![]() 成立,求實數(shù)
成立,求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】以下關(guān)于圓錐曲線的命題中:
①雙曲線![]() 與橢圓
與橢圓![]() 有相同焦點(diǎn);
有相同焦點(diǎn);
②以拋物線的焦點(diǎn)弦(過焦點(diǎn)的直線截拋物線所得的線段)為直徑的圓與拋物線的準(zhǔn)線是相切的;
③設(shè)![]() 、
、![]() 為兩個定點(diǎn),
為兩個定點(diǎn),![]() 為常數(shù),若
為常數(shù),若![]() ,則動點(diǎn)
,則動點(diǎn)![]() 的軌跡為雙曲線;
的軌跡為雙曲線;
④過拋物線![]() 的焦點(diǎn)作直線與拋物線相交于
的焦點(diǎn)作直線與拋物線相交于![]() 、
、![]() ,則使它們的橫坐標(biāo)之和等于5的直線有且只有兩條;
,則使它們的橫坐標(biāo)之和等于5的直線有且只有兩條;
以上命題正確的個數(shù)為( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在直棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 分別是棱
分別是棱![]() ,
,![]() 上的點(diǎn),且
上的點(diǎn),且![]() 平面
平面![]() .
.

(1)證明:![]() ;
;
(2)若![]() 為
為![]() 中點(diǎn),求直線
中點(diǎn),求直線![]() 與直線
與直線![]() 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
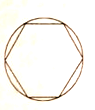
【題目】“割圓術(shù)”是劉徽最突出的數(shù)學(xué)成就之一,他在《九章算術(shù)注》中提出割圓術(shù),并作為計算圓的周長,面積已經(jīng)圓周率的基礎(chǔ),劉徽把圓內(nèi)接正多邊形的面積一直算到了正3072邊形,并由此而求得了圓周率為3.1415和3.1416這兩個近似數(shù)值,這個結(jié)果是當(dāng)時世界上圓周率計算的最精確數(shù)據(jù).如圖,當(dāng)分割到圓內(nèi)接正六邊形時,某同學(xué)利用計算機(jī)隨機(jī)模擬法向圓內(nèi)隨機(jī)投擲點(diǎn),計算得出該點(diǎn)落在正六邊形內(nèi)的頻率為0.8269,那么通過該實驗計算出來的圓周率近似值為(參考數(shù)據(jù):![]() )
)
A. 3.1419B. 3.1417C. 3.1415D. 3.1413
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() .
.
(1)若![]() ,求
,求![]() 的單調(diào)區(qū)間;
的單調(diào)區(qū)間;
(2)若函數(shù)![]() 存在唯一的零點(diǎn)
存在唯一的零點(diǎn)![]() ,且
,且![]() ,則
,則![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]()
(1)若存在正數(shù)![]() ,使
,使![]() 恒成立,求實數(shù)
恒成立,求實數(shù)![]() 的最大值;
的最大值;
(2)設(shè)![]() ,若
,若![]() 沒有零點(diǎn),求實數(shù)
沒有零點(diǎn),求實數(shù)![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com